For anyone curious about the broader landscape of mathematical spaces, it’s fascinating to learn that Uniform Spaces and coarse spaces stand as two contrasting yet complementary generalizations of the familiar metric spaces. When we measure distances using a metric, we can focus on points that are very close together – this is where uniform spaces become crucial. Conversely, we can also be interested in points that are far apart, which is the domain of coarse geometry. Think of uniform and coarse spaces as two sides of the same coin, both extending the idea of metric spaces but in opposite directions along the spectrum of distances from zero to infinity. Both concepts allow us to compare distances between points even without relying on precise numerical measurements.
What is a Uniform Space?
Uniform spaces, along with their counterparts, coarse spaces, are formally defined as pairs $(X, mathcal{U})$, where $X$ is a set and $mathcal{U}$ is a family of subsets of $X times X$ called “entourages.” These entourages always contain the diagonal ${(x,x): x in X}$, representing zero distance. Uniform spaces are governed by a set of axioms that capture the notion of “uniformity”:
(U1) Supersets of Entourages are Entourages: If $U subseteq V subseteq X times X$ and $U in mathcal{U}$, then $V in mathcal{U}$. This means if we have a condition for “closeness” (represented by $U$), any looser condition ($V$) also qualifies as “closeness” in our uniform space.
(U2) Inverse Entourages are Entourages: For every $U in mathcal{U}$, the inverse entourage $-U = {(y,x): (x,y) in U}$ also belongs to $mathcal{U}$. This axiom ensures symmetry in our notion of “closeness”; if $x$ is “close” to $y$, then $y$ is also “close” to $x$.
(U3) Composition of Entourages is in Entourage Family: For each $U in mathcal{U}$, there exists a $V in mathcal{U}$ such that $V+V subseteq U$. Here, $V+V = {(x,z): exists y in X text{ such that } (x,y), (y,z) in V}$. This composition axiom is crucial; it allows us to refine our notion of “closeness.” If being “V-close” twice implies being “U-close,” we establish a consistent structure for uniformity.
Coarse spaces, on the other hand, follow dual axioms, essentially flipping the direction of inclusion in axioms (C1) and (C3), while keeping the symmetry axiom (C2) the same. This duality highlights their opposite nature in generalizing metric spaces.
Morphisms: Uniformly Continuous and Coarse Maps
To further understand these spaces, we need to consider the mappings between them that preserve their structure. In the category of uniform spaces, these mappings are called uniformly continuous maps. A function $f: X to Y$ between uniform spaces $(X, mathcal{U}_X)$ and $(Y, mathcal{U}_Y)$ is uniformly continuous if for every entourage $U in mathcal{U}_Y$ in $Y$, there exists an entourage $V in mathcal{U}_X$ in $X$ such that ${(f(x), f(y)): (x,y) in V} subseteq U$. This definition rigorously captures the idea that the “uniform closeness” of points in $X$ is preserved when mapped to $Y$.
Similarly, for coarse spaces, the structure-preserving mappings are coarse maps. A function $f: X to Y$ between coarse spaces $(X, mathcal{U}_X)$ and $(Y, mathcal{U}_Y)$ is a coarse map if for every entourage $V in mathcal{U}_X$ in $X$, there exists an entourage $U in mathcal{U}_Y$ in $Y$ such that ${(f(x), f(y)): (x,y) in V} subseteq U$. Notice the similarity in form to uniformly continuous maps, emphasizing the parallel yet distinct nature of these concepts.
Why Uniform and Coarse Spaces Matter
The beauty of uniform and coarse spaces lies in their ability to abstract and generalize fundamental concepts from analysis. Long before uniform and coarse spaces were formally defined, mathematicians in analysis were working with $epsilon-delta$ definitions to describe uniformly continuous and coarse behaviors. The introduction of uniform and coarse spaces provided a robust and general framework to study these concepts in a broader context, beyond just metric spaces. They represent the most general structures that allow us to formally discuss uniformly continuous and coarse maps.
Dimension in Uniform and Coarse Spaces
For those interested in deeper questions, the concept of dimension provides a fascinating area of exploration within uniform and coarse spaces. We intuitively understand that the space $mathbb{R}^n$ has dimension $n$, but how do we rigorously define “dimension” in different mathematical categories? Categories like linear spaces, rings, metric spaces, and topological spaces all offer various definitions of dimension, each reflecting different aspects of the space.
Uniform and coarse spaces also have their own notions of dimension, which, true to their nature, exhibit a duality. The uniform dimension $dim(X, mathcal{U})$ of a uniform space $(X, mathcal{U})$ is the smallest number $n$ such that for any entourage $U in mathcal{U}$, there exists an entourage $V in mathcal{U}$ and a cover $mathcal{C}$ of $X$ by sets $C subseteq X$ of diameter less than $V$ where no point of $X$ is contained in more than $n+1$ elements of $mathcal{C}$.
Conversely, the coarse dimension (or Gromov’s asymptotic dimension) $Dim(X, mathcal{U})$ of a coarse space $(X, mathcal{U})$ is the smallest number $n$ such that for any entourage $V in mathcal{U}$, there exist an entourage $U in mathcal{U}$ and a cover $mathcal{C}$ of $X$ by sets $C subseteq X$ of diameter less than $U$ where no point of $X$ is contained in more than $n+1$ elements of $mathcal{C}$.
Notice the subtle but significant shift in quantifiers: uniform dimension considers “small $U$”, while coarse dimension focuses on “large $V$”. This seemingly small change reflects the fundamental duality between these concepts.
Example: The Plane and Bricks
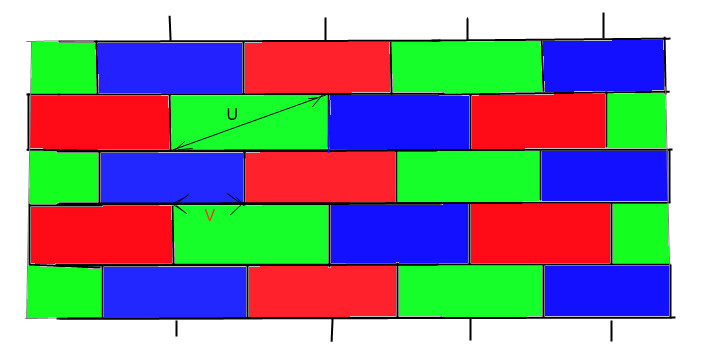The plane covered by bricks sorted into three subfamilies
A simple illustration of these dimensions can be seen in the plane $mathbb{R}^2$. Imagine tiling the plane with bricks. Whether these bricks are small or large, this tiling demonstrates that the plane has both uniform and coarse dimension equal to 2. A significant result in the theories of uniform and coarse dimension confirms that indeed, the uniform and coarse dimension of $mathbb{R}^n$ is $n$. Interestingly, while the coarse dimension of $mathbb{Z}^n$ (the integer lattice) is also $n$, its uniform dimension is zero. On the other hand, the uniform dimension of the cube $[0,1]^n$ is $n$, but its coarse dimension is zero. These examples further highlight the contrasting behaviors and applications of uniform and coarse dimensions.
References:
For a deeper dive into uniform spaces, “General Topology” by Engelking (Chapter 8) is a foundational resource. For coarse spaces, “Lectures on Coarse Geometry” by J. Roe provides a comprehensive introduction.
Alt text for image: Brick wall tiling pattern illustrating the concept of uniform and coarse dimension in a 2-dimensional plane, relevant to uniform space and coarse space concepts.
