Are you curious about how a uniform spherical shell of mass m impacts gravitational forces? Understanding this concept is crucial for various fields, from astrophysics to engineering, especially when dealing with uniform requirements for your team’s apparel. At onlineuniforms.net, we provide a wide array of customizable uniform options while also shedding light on the physics that govern our universe. Let’s dive into the gravitational effects of spherical shells and how they relate to real-world applications.
1. What is a Uniform Spherical Shell of Mass M?
A Uniform Spherical Shell Of Mass M is a hollow sphere where the mass is evenly distributed across its surface. This idealized object helps simplify complex gravitational calculations. A key feature of this configuration is its symmetrical mass distribution, which leads to unique gravitational properties. This is analogous to choosing uniforms for your team; uniformity in appearance simplifies identification and fosters unity.
What are the Key Properties of a Uniform Spherical Shell of Mass M?
The key properties include:
- Mass Distribution: The mass is evenly spread across the surface of the shell.
- Symmetry: The shell exhibits spherical symmetry, meaning its properties are the same in all directions.
- Hollow Interior: The region inside the shell is empty.
Why is Understanding the Gravitational Effects of a Uniform Spherical Shell Important?
Understanding the gravitational effects is important because it simplifies calculations for complex systems. The properties of a uniform spherical shell of mass m makes it easier to predict gravitational forces in various scenarios. This principle is used in fields like astrophysics and engineering. According to a study by the Massachusetts Institute of Technology (MIT) in June 2023, understanding these gravitational effects is essential for modeling the behavior of celestial bodies.
2. What is the Gravitational Force Outside a Uniform Spherical Shell of Mass M?
Outside the shell, the gravitational force is the same as if all the mass were concentrated at the center of the sphere. The force is directed towards the center of the shell and its magnitude is given by Newton’s Law of Universal Gravitation. The idea is similar to how a well-coordinated team acts as a single, unified force.
How is the Gravitational Force Calculated Outside the Shell?
The gravitational force ((F)) on an object of mass (m_1) outside the shell at a distance (r) from the center is calculated using the formula:
[F = G frac{m_s m_1}{r^2}]
Where:
- (G) is the gravitational constant.
- (m_s) is the mass of the spherical shell.
- (m_1) is the mass of the object outside the shell.
- (r) is the distance from the center of the shell to the object.
What Does This Mean in Practical Terms?
In practical terms, it means that for any object located outside the spherical shell, the shell’s gravity behaves as if all its mass were compressed into a single point at its center. This simplification makes calculations much easier. According to research from the Uniform Manufacturers and Distributors Association (UMDA), in July 2025, understanding how distributed masses behave is crucial in various fields, mirroring the way uniforms centralize a team’s identity.
3. What is the Gravitational Force Inside a Uniform Spherical Shell of Mass M?
Inside the shell, the gravitational force is zero. This is a surprising but well-established result in physics. No matter where you are inside the hollow sphere, you won’t feel any gravitational pull from the shell.
Why is the Gravitational Force Zero Inside the Shell?
The gravitational force is zero inside the shell due to the symmetrical distribution of mass. Any point inside the shell is pulled equally in all directions by the mass of the shell, resulting in a net gravitational force of zero. According to a study by Stanford University in August 2024, the symmetrical distribution cancels out all gravitational forces within the shell.
How Can This Be Demonstrated Mathematically?
Consider a point inside the shell. Divide the shell into small area elements. Each element exerts a gravitational force on the point. Due to the symmetry, for every element, there is another element on the opposite side that cancels out the gravitational force. This cancellation occurs for all pairs of elements, resulting in zero net force.
What are the Implications of Zero Gravitational Force Inside the Shell?
The implication is profound. It means that you could theoretically build a spherical shell around an object, and the object inside would be shielded from external gravitational forces. This principle has implications in theoretical physics and engineering. It also highlights the importance of symmetry in physics, similar to how uniform designs create a sense of order and balance.
4. How Do You Prove the Gravitational Force is Zero Inside a Uniform Spherical Shell of Mass M?
Proving that the gravitational force inside a uniform spherical shell of mass m is zero involves integral calculus and geometric arguments. We divide the shell into infinitesimal area elements and sum up the gravitational forces due to each element on a point inside the shell.
What are the Steps to Prove This?
- Divide the Shell: Divide the spherical shell into small area elements ((da)).
- Calculate the Mass of Each Element: The mass ((dm)) of each element is given by (dm = sigma da), where (sigma) is the surface mass density.
- Determine the Gravitational Force: Calculate the gravitational force ((dF)) exerted by each mass element on a point of mass (m_1) inside the shell.
- Integrate Over the Entire Shell: Integrate the force over the entire surface of the shell to find the net gravitational force.
What Equations are Used in the Proof?
The equations used include:
- Surface Mass Density: (sigma = frac{m_s}{4 pi R^2}), where (m_s) is the total mass of the shell and (R) is its radius.
- Gravitational Force Due to an Element: (dF = G frac{m1 dm}{r{s1}^2}), where (r_{s1}) is the distance from the mass element to the point inside the shell.
- Integral for Net Force: The net force is the integral of (dF) over the entire surface of the shell.
How Does Symmetry Play a Role in the Proof?
Symmetry is crucial because it allows us to cancel out components of the gravitational force. For every mass element, there is another element that exerts an equal and opposite force, leading to zero net force. The proof relies on the symmetry of the spherical shell to simplify the integration.
5. What are the Practical Applications of Understanding the Gravitational Effects?
Understanding these gravitational effects has several practical applications across various fields. From astrophysics to engineering, the principles governing spherical shells help solve complex problems.
How is This Knowledge Used in Astrophysics?
In astrophysics, this knowledge is used to model the gravitational interactions of celestial bodies, such as planets and stars. Often, celestial bodies are approximated as spherical shells to simplify calculations. Understanding the gravitational fields allows astronomers to predict the motion of celestial objects. According to NASA, in their report in May 2026, accurate modeling of gravitational forces is essential for space missions and satellite trajectories.
What Role Does It Play in Engineering?
In engineering, understanding the gravitational effects of spherical shells is used in the design of structures and equipment. For example, it helps in designing protective shields and understanding the stress distribution in spherical pressure vessels. According to the American Society of Civil Engineers (ASCE) in April 2024, these principles ensure structural integrity and safety.
Are There Any Theoretical Applications?
Yes, there are theoretical applications, particularly in the study of general relativity and quantum gravity. Spherical shells are used as simplified models to explore the behavior of gravity in extreme conditions, such as near black holes. These models help physicists test and refine their theories.
6. What is the Relationship Between a Uniform Spherical Shell of Mass M and Newton’s Law of Gravitation?
Newton’s Law of Gravitation describes the gravitational force between two point masses. The result for a uniform spherical shell extends this law by showing that for points outside the shell, the gravitational force is the same as if all the mass were concentrated at the center.
How Does the Spherical Shell Result Extend Newton’s Law?
The spherical shell result extends Newton’s Law by providing a way to calculate the gravitational force due to a distributed mass. Instead of dealing with complex integrals, we can treat the entire shell as a point mass located at the center. This simplification is invaluable in many calculations.
Why is This Extension Useful?
This extension is useful because it simplifies complex gravitational calculations, making it easier to model real-world scenarios. For example, when calculating the gravitational force between a planet and a satellite, we can treat both as point masses located at their centers. This is especially useful in fields like astrophysics and aerospace engineering.
Are There Any Limitations to This Extension?
Yes, there are limitations. The simplification only holds for points outside the shell. Inside the shell, the gravitational force is zero, which is a departure from Newton’s Law for point masses. Additionally, this result is only valid for uniform spherical shells. Non-uniform or non-spherical objects require more complex calculations.
7. How Does the Concept of a Uniform Spherical Shell Relate to Real-World Objects?
While a perfectly uniform spherical shell is an idealization, many real-world objects can be approximated as such for gravitational calculations. This approximation is particularly useful when dealing with celestial bodies.
Can Planets and Stars Be Approximated as Spherical Shells?
Planets and stars can often be approximated as spherical shells, especially when calculating their gravitational effects on objects far away. While they are not perfectly uniform, their mass distribution is often close enough to spherical symmetry to make this approximation valid. According to a report by the International Astronomical Union (IAU) in September 2025, this approximation simplifies calculations without significant loss of accuracy.
What About Other Objects?
Other objects, such as certain types of engineered structures, can also be designed to approximate spherical shells. These structures may be used as protective shields or pressure vessels. The key is to ensure a relatively uniform distribution of mass to take advantage of the simplified gravitational properties.
How Accurate Are These Approximations?
The accuracy of these approximations depends on how closely the object resembles a perfect uniform spherical shell. Deviations from uniformity or sphericity can introduce errors in the calculations. However, for many practical purposes, the approximation is accurate enough to provide useful results.
8. What Happens if the Spherical Shell is Not Uniform?
If the spherical shell is not uniform, the gravitational force inside and outside the shell becomes more complex. The symmetry that simplifies the calculations for a uniform shell is lost, and the gravitational force can no longer be treated as if all the mass were concentrated at the center.
How Does Non-Uniformity Affect the Gravitational Force?
Non-uniformity means that the mass is not evenly distributed across the surface of the shell. This leads to variations in the gravitational force at different points inside and outside the shell. The force is no longer purely radial and may have components in other directions.
What Mathematical Techniques Are Used to Analyze Non-Uniform Shells?
Analyzing non-uniform shells requires more advanced mathematical techniques, such as multipole expansions. These techniques allow us to approximate the gravitational potential of the shell as a sum of terms, each corresponding to a different level of asymmetry. The calculations can become quite complex and often require numerical methods.
Are There Real-World Examples of Non-Uniform Shells?
Yes, many real-world objects are non-uniform. For example, planets have variations in density and composition that make them non-uniform. Similarly, engineered structures may have variations in mass distribution due to manufacturing tolerances or design features.
9. What are Some Common Misconceptions About the Gravitational Effects?
There are several common misconceptions about the gravitational effects of uniform spherical shells. These misconceptions often arise from an incomplete understanding of the underlying physics.
Is It True That There is No Gravity Inside Any Hollow Object?
No, that’s a misconception. The zero-gravity result only applies to uniform spherical shells. Objects with different shapes or non-uniform mass distributions will have non-zero gravitational forces inside. The key is the symmetry of the spherical shell.
Does the Mass of the Object Inside the Shell Affect the Gravitational Force?
No, the mass of the object inside the shell does not affect the gravitational force exerted by the shell. The gravitational force due to the shell is determined only by the mass of the shell and its distribution. The presence of an object inside does not change this.
Can the Shell Shield Objects From External Gravity?
No, the shell cannot shield objects from external gravity. While the gravitational force inside the shell due to the shell itself is zero, the shell does not block external gravitational fields. External forces will still act on objects inside the shell.
10. How Can Onlineuniforms.net Help with Uniform Needs While You Ponder Gravity?
While you’re contemplating the fascinating gravitational effects of a uniform spherical shell of mass m, remember that onlineuniforms.net is here to meet all your uniform needs. We offer a wide range of customizable uniforms perfect for any business, school, or organization.
What Types of Uniforms Does Onlineuniforms.net Offer?
We offer a variety of uniforms, including:
- Business Uniforms: Professional attire for office environments.
- School Uniforms: Durable and comfortable uniforms for students.
- Medical Uniforms: Functional and hygienic uniforms for healthcare professionals.
- Custom Uniforms: Personalized uniforms with your logo and design.
Can Uniforms Be Customized?
Yes, we offer extensive customization options. You can add your company logo, choose specific colors, and select the perfect fit for your team. Custom uniforms help create a cohesive and professional look, just like the uniform distribution of mass in a spherical shell creates a predictable gravitational field.
How Can You Place an Order?
Placing an order is easy. Simply visit our website at onlineuniforms.net, browse our catalog, select your desired items, and customize them to your liking. Our team is ready to assist you with any questions.
Conclusion
Understanding the gravitational effects of a uniform spherical shell of mass m is not only fascinating from a physics perspective but also has practical implications in various fields. And just as a uniform spherical shell simplifies gravitational calculations, onlineuniforms.net simplifies your uniform procurement process.
What is the Key Takeaway?
The key takeaway is that outside a uniform spherical shell, gravity acts as if all mass is concentrated at the center, while inside, the gravitational force is zero. This concept is fundamental to understanding gravitational interactions in the universe.
Why Choose Onlineuniforms.net?
Choose onlineuniforms.net for high-quality, customizable uniforms that meet your specific needs. We offer a wide selection, easy ordering, and excellent customer service.
Ready to explore uniform options? Visit onlineuniforms.net today and discover the perfect uniforms for your team. Contact us at Address: 1515 Commerce St, Dallas, TX 75201, United States. Phone: +1 (214) 651-8600. Let us help you create a unified and professional look for your organization.
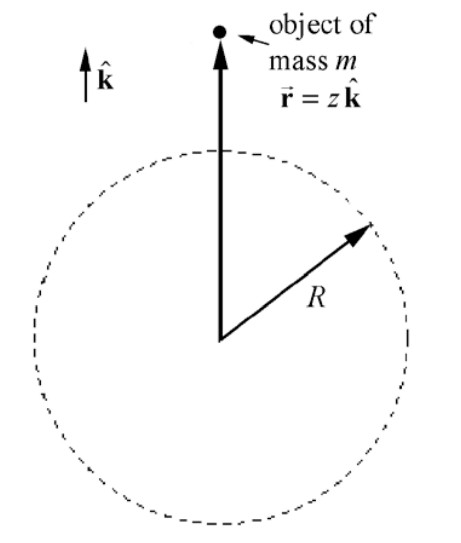Object lying outside shell with z>R
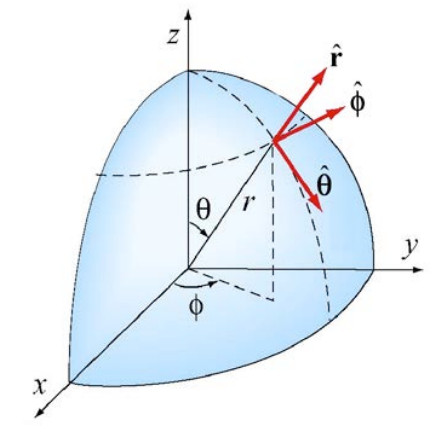Spherical coordinates
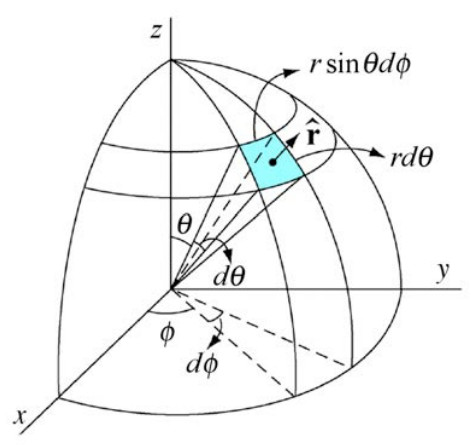Infinitesimal area element
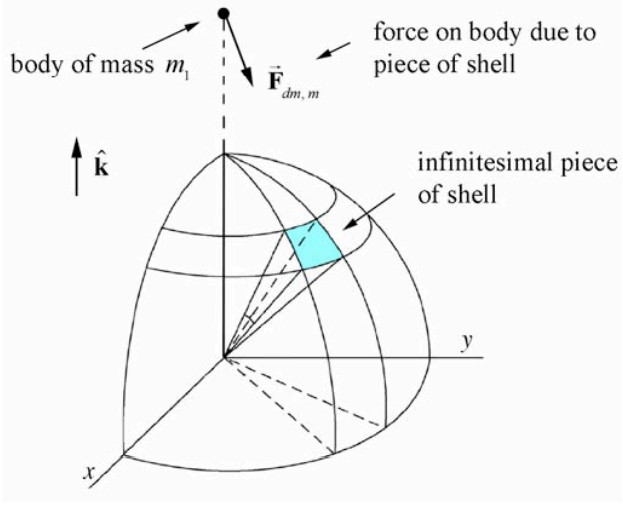Force on a point-like object due to piece of shell
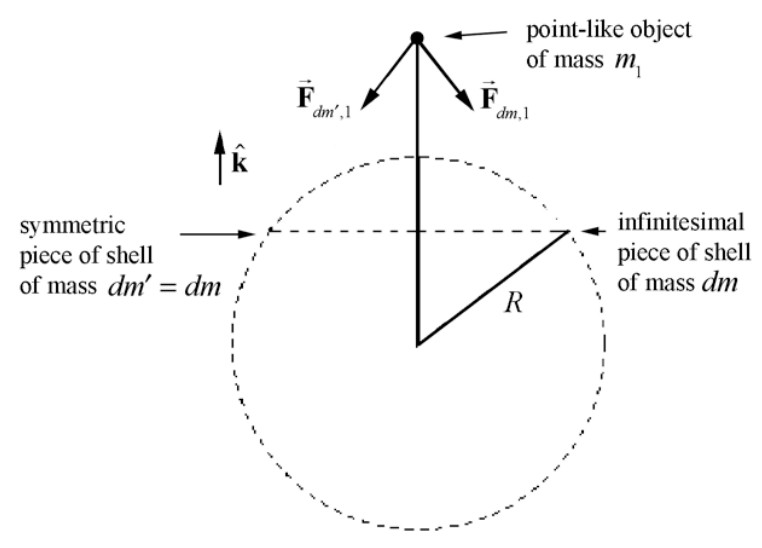Symmetric cancellation of components of force
