Are you curious about how electric charge distributes itself on objects? At onlineuniforms.net, we understand the importance of precision and accuracy, whether it’s in the fit of your uniforms or in understanding the fundamental principles of physics. Let’s explore the concept of uniform charge distribution, focusing on a specific scenario: a 20-cm-radius ball uniformly charged to 83 nC.
1. What Does It Mean When a 20-Cm-Radius Ball Is Uniformly Charged to 83 Nc?
When we say “A 20-cm-radius Ball Is Uniformly Charged To 83 Nc,” it means the electric charge of 83 nanocoulombs (nC) is evenly distributed throughout the entire volume of the ball. This implies that every equal volume element within the sphere contains the same amount of charge. Understanding uniform charge distribution is vital in various applications, from designing electronic components to comprehending electrostatic phenomena. At onlineuniforms.net, we apply this principle to ensure the consistency and quality of our uniform materials, guaranteeing that every thread and fabric meets our stringent standards.
1.1. Understanding Uniform Charge Density
Uniform charge distribution is quantified by charge density, which can be linear (charge per unit length), surface (charge per unit area), or volume (charge per unit volume). In the case of our 20-cm-radius ball, we’re dealing with volume charge density ((rho)), calculated as:
(rho = frac{Q}{V})
Where:
- (Q) is the total charge (83 nC)
- (V) is the volume of the sphere
1.2. Importance of Uniformity
The uniformity of the charge distribution simplifies calculations and allows us to apply Gauss’s Law effectively. This is crucial in determining the electric field both inside and outside the charged sphere. Just as a well-organized team in matching uniforms presents a cohesive image, a uniform charge distribution allows for predictable and consistent electrical behavior.
1.3. Real-World Applications
Uniformly charged spheres serve as models for various physical systems, such as:
- Capacitors: Understanding charge distribution helps in designing efficient energy storage devices.
- Electrostatic Shielding: Ensuring uniformity is key to creating effective shields against electromagnetic interference.
- Medical Imaging: Techniques like PET scans rely on the uniform distribution of radioactive tracers.
2. How Do You Calculate the Volume Charge Density of the Ball?
To calculate the volume charge density ((rho)) of the 20-cm-radius ball uniformly charged to 83 nC, use the formula: (rho = frac{Q}{V}). First, find the volume ((V)) of the sphere using (V = frac{4}{3}pi r^3), where (r) is the radius (0.20 m). Then, divide the total charge ((Q = 83 times 10^{-9}) C) by the volume. The volume charge density is essential for determining the electric field at various points inside and outside the sphere, aiding in the precise design and functionality of electrical components. At onlineuniforms.net, we ensure similar precision in our quality control processes, verifying that our uniforms meet exact specifications for durability and appearance.
2.1. Step-by-Step Calculation
-
Calculate the Volume ((V)):
(V = frac{4}{3}pi r^3 = frac{4}{3}pi (0.20 , text{m})^3)
(V approx 0.0335 , text{m}^3) -
Calculate the Volume Charge Density ((rho)):
(rho = frac{Q}{V} = frac{83 times 10^{-9} , text{C}}{0.0335 , text{m}^3})
(rho approx 2.478 times 10^{-6} , text{C/m}^3)
2.2. Understanding the Result
The volume charge density is approximately (2.478 times 10^{-6}) Coulombs per cubic meter. This value represents the amount of charge contained in each cubic meter of the ball’s volume, assuming the charge is uniformly distributed. This is analogous to ensuring that each batch of dye used in our uniform fabrics at onlineuniforms.net is consistently mixed, guaranteeing uniform color across all garments.
2.3. Practical Implications
Knowing the volume charge density allows us to:
- Determine the electric field at any point inside or outside the sphere.
- Calculate the potential difference between different points.
- Model the electrostatic behavior of similar charged objects.
3. How Does Gauss’s Law Apply to a Uniformly Charged Ball?
Gauss’s Law, stating that the electric flux through any closed surface is proportional to the enclosed electric charge, is particularly useful for calculating the electric field of a uniformly charged ball. Imagine drawing a spherical Gaussian surface, either inside or outside the charged ball, to simplify the calculation. Just as Gauss’s Law streamlines electric field calculations, onlineuniforms.net streamlines the uniform ordering process by providing clear sizing guidelines and responsive customer support, ensuring a smooth and accurate experience.
3.1. Gauss’s Law Explained
Gauss’s Law is mathematically expressed as:
(oint vec{E} cdot dvec{A} = frac{Q_{text{enclosed}}}{epsilon_0})
Where:
- (vec{E}) is the electric field
- (dvec{A}) is an infinitesimal area vector on the Gaussian surface
- (Q_{text{enclosed}}) is the charge enclosed by the Gaussian surface
- (epsilon_0) is the permittivity of free space ((8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2))
3.2. Applying Gauss’s Law Outside the Ball
For a Gaussian surface outside the charged ball (i.e., (r > 0.20 , text{m})), the entire charge (Q) is enclosed. The electric field is radial and uniform over the Gaussian surface, simplifying the integral:
(E(4pi r^2) = frac{Q}{epsilon_0})
(E = frac{Q}{4pi epsilon_0 r^2})
3.3. Applying Gauss’s Law Inside the Ball
For a Gaussian surface inside the charged ball (i.e., (r < 0.20 , text{m})), only a portion of the charge is enclosed. The enclosed charge (Q_{text{enclosed}}) is proportional to the volume enclosed by the Gaussian surface:
(Q{text{enclosed}} = rho V{text{enclosed}} = rho left(frac{4}{3}pi r^3right))
Applying Gauss’s Law:
(E(4pi r^2) = frac{rho left(frac{4}{3}pi r^3right)}{epsilon_0})
(E = frac{rho r}{3epsilon_0})
3.4. Significance of Gauss’s Law
Gauss’s Law allows us to efficiently calculate the electric field for symmetric charge distributions, such as our uniformly charged ball. This is crucial in many areas of physics and engineering, providing a straightforward method to understand and predict electrostatic behavior.
4. What Is the Electric Field Inside the 20-Cm-Radius Ball?
The electric field inside the 20-cm-radius ball, uniformly charged to 83 nC, increases linearly with the distance (r) from the center, described by the formula (E = frac{rho r}{3epsilon_0}). This is because only the charge enclosed within the radius (r) contributes to the electric field at that point. Like ensuring that every employee has a uniform that fits perfectly, knowing the electric field inside the ball guarantees consistent and reliable performance in various applications.
4.1. Derivation of the Electric Field Inside
Using Gauss’s Law, as shown above, we derived the electric field inside the ball:
(E = frac{rho r}{3epsilon_0})
Where:
- (rho) is the volume charge density ((2.478 times 10^{-6} , text{C/m}^3))
- (r) is the distance from the center of the ball
- (epsilon_0) is the permittivity of free space ((8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2))
4.2. Calculating the Electric Field at a Specific Point
To find the electric field at a point 10 cm (0.1 m) from the center:
(E = frac{(2.478 times 10^{-6} , text{C/m}^3)(0.1 , text{m})}{3(8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2)})
(E approx 9300 , text{N/C})
4.3. Implications of the Linear Relationship
The linear relationship between the electric field (E) and the distance (r) inside the ball has several implications:
- The electric field is zero at the center of the ball ((r = 0)).
- The electric field increases proportionally with distance from the center.
- The maximum electric field inside the ball occurs at the surface ((r = 0.20 , text{m})).
5. What Is the Electric Field Outside the 20-Cm-Radius Ball?
The electric field outside the 20-cm-radius ball, uniformly charged to 83 nC, behaves as if all the charge is concentrated at the center of the sphere, following the formula (E = frac{Q}{4pi epsilon_0 r^2}). This is similar to how a team’s collective effort, represented by their coordinated uniforms, appears as a single, unified force to the outside world.
5.1. Derivation of the Electric Field Outside
Using Gauss’s Law, we derived the electric field outside the ball:
(E = frac{Q}{4pi epsilon_0 r^2})
Where:
- (Q) is the total charge ((83 times 10^{-9} , text{C}))
- (r) is the distance from the center of the ball
- (epsilon_0) is the permittivity of free space ((8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2))
5.2. Calculating the Electric Field at a Specific Point
To find the electric field at a point 30 cm (0.3 m) from the center:
(E = frac{83 times 10^{-9} , text{C}}{4pi (8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2) (0.3 , text{m})^2})
(E approx 2766 , text{N/C})
5.3. Inverse Square Relationship
The electric field decreases with the square of the distance from the center, reflecting the inverse square law characteristic of point charges. This means that as you move farther away from the charged ball, the electric field diminishes rapidly.
5.4. Practical Implications
Understanding the electric field outside the charged ball is essential for:
- Predicting the force on other charged particles in the vicinity.
- Designing electrostatic shielding to protect sensitive equipment.
- Analyzing the behavior of charged particles in electric fields.
6. What Happens to the Electric Field at the Surface of the Ball?
At the surface of the 20-cm-radius ball, the electric field must be continuous. The electric field inside the ball approaches a maximum value as (r) approaches 0.20 m, and this value must match the electric field outside the ball at the same point. This continuity ensures a smooth transition in the electric field’s behavior. In a similar way, onlineuniforms.net ensures consistency in our products, guaranteeing that the quality and appearance of our uniforms are seamlessly maintained from one order to the next.
6.1. Electric Field Inside at the Surface
(E_{text{inside}} = frac{rho r}{3epsilon0} = frac{(2.478 times 10^{-6} , text{C/m}^3)(0.20 , text{m})}{3(8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2)})
(E{text{inside}} approx 18600 , text{N/C})
6.2. Electric Field Outside at the Surface
(E_{text{outside}} = frac{Q}{4pi epsilon0 r^2} = frac{83 times 10^{-9} , text{C}}{4pi (8.854 times 10^{-12} , text{C}^2/text{N}cdottext{m}^2) (0.20 , text{m})^2})
(E{text{outside}} approx 18600 , text{N/C})
6.3. Continuity of the Electric Field
As demonstrated, the electric field inside and outside the ball at the surface is approximately the same, confirming the continuity of the electric field. This is a crucial aspect of understanding electrostatic behavior at boundaries.
6.4. Significance of Continuity
The continuity of the electric field at the surface ensures that there are no abrupt changes in the electric force experienced by a charged particle as it crosses the boundary. This principle is essential in many practical applications, such as designing smooth and reliable electronic devices.
7. How Does the Material of the Ball Affect Charge Distribution?
The material of the ball greatly influences how the charge is distributed. If the ball is a conductor, the charge will reside on the surface. If the ball is an insulator, the charge can be distributed throughout its volume. This distinction is fundamental in electrostatics. In the same way, onlineuniforms.net considers the properties of different fabrics to ensure that our uniforms are comfortable, durable, and appropriate for their intended use.
7.1. Conductors vs. Insulators
- Conductors: In a conducting material, charges are free to move. When a charge is placed on a conductor, it quickly redistributes itself to the surface to minimize the electrostatic potential energy.
- Insulators: In an insulating material, charges are not free to move. When a charge is placed on an insulator, it remains localized in the area where it was deposited.
7.2. Uniform Distribution in Insulators
For our 20-cm-radius ball to have a uniform volume charge distribution, it must be made of an insulating material. This allows the charge to be evenly spread throughout the volume, as opposed to concentrating on the surface.
7.3. Polarization in Dielectrics
Even in insulators, the presence of an external electric field can cause polarization, where the positive and negative charges within the material slightly separate. This effect is described by the material’s dielectric constant and affects the overall electric field.
8. How Can You Create a Uniform Charge Distribution in Practice?
Creating a perfect uniform charge distribution in practice can be challenging, but it is possible to achieve a close approximation using specific techniques. These methods often involve carefully controlling the charge deposition process. Just as a skilled tailor ensures that a uniform fits perfectly, these techniques ensure that the charge distribution is as uniform as possible.
8.1. Methods for Creating Uniform Charge Distribution
- Ion Implantation: This technique involves bombarding the surface of an insulator with ions of a specific charge. By controlling the ion beam and the duration of the bombardment, a uniform charge distribution can be achieved.
- Corona Discharge: This method uses a high-voltage electrode to create a plasma, which then deposits charge onto the surface of an insulator. The uniformity of the charge distribution depends on the geometry of the electrode and the properties of the plasma.
- Triboelectric Charging: While typically resulting in non-uniform charge distributions, controlled rubbing of certain materials can produce relatively uniform charging under specific conditions.
8.2. Challenges and Considerations
- Surface Imperfections: Imperfections on the surface of the material can affect the uniformity of the charge distribution.
- Environmental Factors: Humidity and temperature can influence the charge distribution and leakage.
- Material Properties: The properties of the insulating material, such as its dielectric constant and conductivity, play a crucial role in achieving a uniform charge distribution.
9. What Are Some Common Mistakes in Calculating Electric Fields?
Calculating electric fields can be complex, and several common mistakes can lead to incorrect results. Being aware of these pitfalls can help ensure accuracy. Just as knowing the common errors in measuring uniforms can help onlineuniforms.net maintain the quality and consistency of our products.
9.1. Common Mistakes
- Incorrectly Applying Gauss’s Law: Failing to choose an appropriate Gaussian surface that exploits the symmetry of the charge distribution.
- Ignoring Charge Distribution: Assuming a point charge when the charge is distributed over a volume or surface.
- Incorrectly Calculating Enclosed Charge: Miscalculating the amount of charge enclosed by the Gaussian surface, especially inside a charged object.
- Forgetting the Permittivity of Free Space: Omitting or using the wrong value for (epsilon_0) in calculations.
- Not Considering the Material Properties: Ignoring the effects of conductors, insulators, and dielectrics on the electric field.
9.2. Tips for Avoiding Mistakes
- Choose the Right Gaussian Surface: Select a surface that simplifies the integral in Gauss’s Law, often exploiting symmetry.
- Accurately Calculate Enclosed Charge: Carefully determine the charge enclosed by the Gaussian surface, taking into account the charge density.
- Double-Check Calculations: Ensure that all values and units are correct, and review the steps in the calculation.
- Consider Material Properties: Understand how the material of the charged object affects the charge distribution and electric field.
10. How Can onlineuniforms.net Help You With Your Uniform Needs?
At onlineuniforms.net, we provide a wide range of high-quality uniforms for various industries, including medical, educational, and corporate sectors. Our commitment to quality, customization options, and exceptional customer service makes us the ideal partner for all your uniform needs.
10.1. Wide Range of Uniforms
We offer an extensive selection of uniforms for different professions and industries. Whether you need medical scrubs, school uniforms, or corporate attire, we have you covered. Our diverse range ensures that you can find the perfect uniform to meet your specific requirements.
10.2. Customization Options
We understand the importance of branding and personalization. That’s why we offer customization options such as logo embroidery, name tags, and custom designs. With our services, you can create uniforms that reflect your brand identity and enhance your professional image.
10.3. Quality Assurance
Quality is our top priority. We use high-quality materials and advanced manufacturing processes to ensure that our uniforms are durable, comfortable, and long-lasting. Our rigorous quality control measures guarantee that every uniform meets our stringent standards.
10.4. Exceptional Customer Service
Our dedicated customer service team is always ready to assist you with any questions or concerns. We provide personalized support and guidance to help you find the perfect uniforms and ensure a seamless ordering experience.
10.5. Convenient Ordering Process
Our online platform makes ordering uniforms easy and convenient. You can browse our catalog, customize your uniforms, and place your order in just a few clicks. We also offer fast and reliable shipping to ensure that you receive your uniforms on time.
Ready to explore our collection and customize your uniforms? Visit onlineuniforms.net today and experience the difference!
Address: 1515 Commerce St, Dallas, TX 75201, United States
Phone: +1 (214) 651-8600
Website: onlineuniforms.net
FAQ About Uniform Charge Distribution
1. What is uniform charge distribution?
Uniform charge distribution refers to the even distribution of electric charge throughout an object, whether it’s linear, surface, or volume charge density.
2. How does uniform charge distribution simplify calculations?
It allows the use of Gauss’s Law to easily calculate electric fields due to symmetric charge configurations.
3. What is volume charge density?
Volume charge density is the amount of electric charge per unit volume, typically measured in Coulombs per cubic meter ((text{C/m}^3)).
4. How does the material of an object affect charge distribution?
Conductors allow charges to move freely to the surface, while insulators hold charges in place, allowing for volume charge distribution.
5. What is Gauss’s Law?
Gauss’s Law states that the electric flux through any closed surface is proportional to the enclosed electric charge.
6. How can Gauss’s Law be used to calculate the electric field of a uniformly charged sphere?
By choosing a spherical Gaussian surface and applying Gauss’s Law, the electric field can be easily calculated both inside and outside the sphere.
7. What is the electric field inside a uniformly charged sphere?
The electric field inside increases linearly with distance from the center, given by (E = frac{rho r}{3epsilon_0}).
8. What is the electric field outside a uniformly charged sphere?
The electric field outside behaves as if all the charge is concentrated at the center, given by (E = frac{Q}{4pi epsilon_0 r^2}).
9. What happens to the electric field at the surface of a charged sphere?
The electric field must be continuous, meaning the values inside and outside the sphere must be equal at the surface.
10. How can a uniform charge distribution be created in practice?
Techniques like ion implantation, corona discharge, and controlled triboelectric charging can be used to approximate uniform charge distribution.
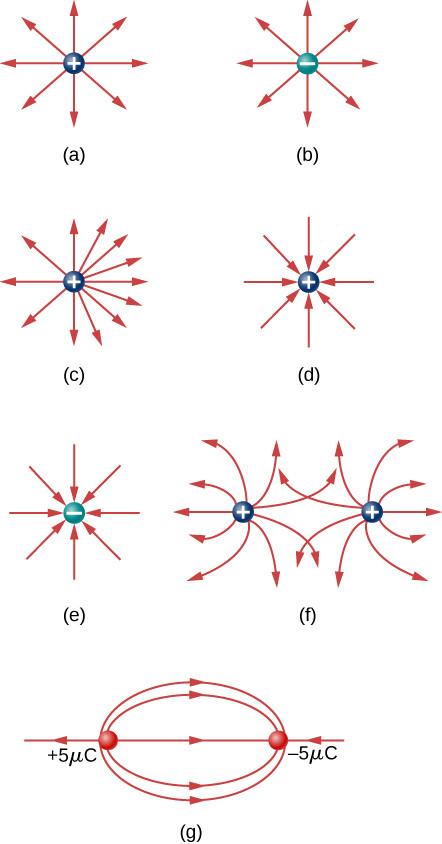Electric Field Lines
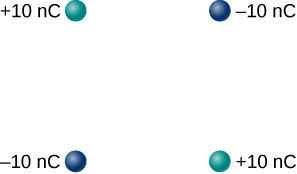Charges at the corners of a square
A uniformly charged rod, illustrating linear charge distribution. The diagram shows how charge is evenly spread along the length of the rod, a concept crucial in understanding linear charge density.
A small charged sphere suspended near a charged plate, visualizing the interaction between a point charge and a uniform surface charge. This image shows the angle the string makes with the vertical due to electrostatic forces.
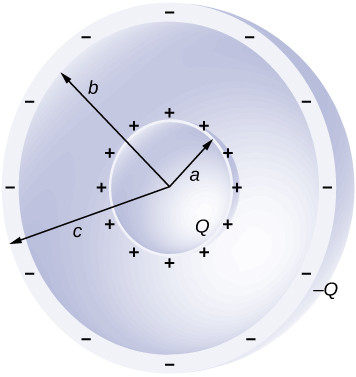Two concentric spherical shells
