A Uniform Magnetic Field Is Perpendicular and plays a crucial role in various scientific and industrial applications. Are you looking for reliable and stylish uniforms for your business, school, or organization? Look no further than onlineuniforms.net! We offer a wide range of high-quality uniforms with customization options to meet your specific needs.
1. What Is a Uniform Magnetic Field and Its Significance?
A uniform magnetic field is perpendicular is a region where the magnetic field strength and direction are the same at every point. This is crucial for many applications. This type of field is essential in many applications.
Understanding Uniform Magnetic Fields
A uniform magnetic field is characterized by its consistent strength and direction throughout a given area. This uniformity simplifies the analysis and control of charged particle motion within the field.
- Definition: A region where the magnetic field has the same magnitude and direction at every point.
- Importance: Essential for controlled experiments and industrial applications.
Key Properties of Uniform Magnetic Fields
Several properties define uniform magnetic fields, making them invaluable in scientific and technological applications.
- Constant Magnitude: The magnetic field strength remains the same at all points.
- Consistent Direction: The magnetic field lines are parallel and equally spaced.
- Predictable Interactions: Charged particles experience a consistent force, simplifying calculations and applications.
2. How Does a Charged Particle Move in a Uniform Magnetic Field That Is Perpendicular?
When a charged particle moves perpendicular to a uniform magnetic field, it experiences a force that causes it to move in a circular path. The magnetic force acts as the centripetal force, keeping the particle in its orbit.
Circular Motion Explained
The interaction between the charged particle and the magnetic field results in circular motion.
- Magnetic Force as Centripetal Force: The magnetic force [latex]F = qvB[/latex] provides the necessary centripetal force [latex]F_c = frac{mv^2}{r}[/latex].
- Radius of the Circular Path: The radius [latex]r[/latex] of the circular path is determined by the equation [latex]r = frac{mv}{qB}[/latex], where [latex]m[/latex] is the mass of the particle, [latex]v[/latex] is its velocity, [latex]q[/latex] is the charge, and [latex]B[/latex] is the magnetic field strength.
Factors Affecting the Circular Path
Several factors influence the characteristics of the circular motion of a charged particle in a uniform magnetic field.
| Factor | Effect on Radius (r) |
|---|---|
| Particle Mass (m) | Larger mass increases the radius. |
| Particle Velocity (v) | Higher velocity increases the radius. |
| Particle Charge (q) | Greater charge decreases the radius. |
| Magnetic Field (B) | Stronger magnetic field decreases the radius. |
Mathematical Representation
The motion of a charged particle in a uniform magnetic field can be described mathematically.
- Magnetic Force: [latex]vec{F} = q(vec{v} times vec{B})[/latex]
- Centripetal Force: [latex]F_c = frac{mv^2}{r}[/latex]
- Radius of Circular Path: [latex]r = frac{mv}{qB}[/latex]
- Period of Revolution: [latex]T = frac{2pi m}{qB}[/latex]
- Angular Velocity: [latex]omega = frac{qB}{m}[/latex]
This table illustrates how the radius [latex]r[/latex] is affected by the mass [latex]m[/latex], velocity [latex]v[/latex], charge [latex]q[/latex], and magnetic field [latex]B[/latex].
3. What Happens If The Velocity Is Not Exactly Perpendicular to the Magnetic Field?
If the velocity of the charged particle is not exactly perpendicular to the magnetic field, the motion becomes helical. The component of velocity parallel to the field results in uniform motion along the field lines, while the perpendicular component causes circular motion.
Understanding Helical Motion
Helical motion is a combination of circular motion and linear motion.
- Parallel Component: The velocity component parallel to the magnetic field ([latex]v_{parallel} = v cos theta[/latex]) results in motion along the field lines.
- Perpendicular Component: The velocity component perpendicular to the magnetic field ([latex]v_{perp} = v sin theta[/latex]) causes circular motion.
- Helical Path: The combination of these motions results in a helical path.
Factors Defining Helical Motion
The characteristics of helical motion are determined by several factors.
| Factor | Description |
|---|---|
| Pitch (p) | The distance between adjacent turns of the helix, [latex]p = v_{parallel} T[/latex]. |
| Radius (r) | The radius of the circular component, [latex]r = frac{mv_{perp}}{qB}[/latex]. |
| Angle ([latex]theta[/latex]) | The angle between the velocity vector and the magnetic field. |
Applications of Helical Motion
Helical motion is utilized in various applications.
- Magnetic Confinement: Used in fusion reactors to confine plasma.
- Particle Physics: Helps in analyzing the momentum and charge of particles in detectors.
- Mass Spectrometry: Separates ions based on their mass-to-charge ratio.
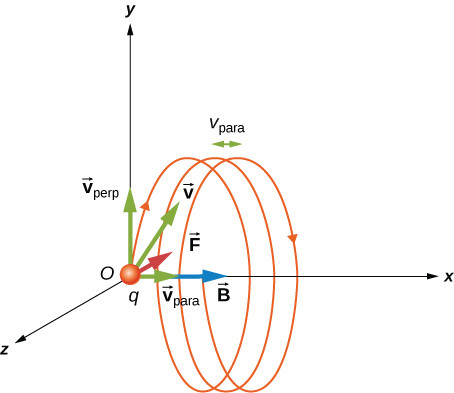 Helical motion of a charged particle in a uniform magnetic field, showcasing the components of velocity parallel and perpendicular to the field
Helical motion of a charged particle in a uniform magnetic field, showcasing the components of velocity parallel and perpendicular to the field
4. What Is the Radius of the Circular Motion of a Charged Particle?
The radius of the circular motion of a charged particle in a uniform magnetic field can be determined using the formula [latex]r = frac{mv}{qB}[/latex]. This radius depends on the particle’s mass, velocity, charge, and the strength of the magnetic field.
Derivation of the Radius Formula
The radius formula is derived from equating the magnetic force and the centripetal force.
- Magnetic Force: [latex]F = qvB[/latex]
- Centripetal Force: [latex]F_c = frac{mv^2}{r}[/latex]
- Equating the Forces: [latex]qvB = frac{mv^2}{r}[/latex]
- Solving for r: [latex]r = frac{mv}{qB}[/latex]
Factors Influencing the Radius
The radius of the circular path is influenced by the following factors:
- Mass (m): A heavier particle will have a larger radius, assuming the same charge, velocity, and magnetic field.
- Velocity (v): A faster particle will also have a larger radius, as it requires more force to keep it in the same circular path.
- Charge (q): A particle with a larger charge will experience a greater magnetic force, resulting in a smaller radius.
- Magnetic Field (B): A stronger magnetic field will exert a greater force on the particle, causing it to move in a smaller circle.
Example Calculation
Let’s consider a proton ([latex]q = 1.602 times 10^{-19}[/latex] C, [latex]m = 1.672 times 10^{-27}[/latex] kg) moving at a speed of [latex]5 times 10^6[/latex] m/s in a magnetic field of 1.5 T. The radius of its circular path would be:
[latex]r = frac{(1.672 times 10^{-27}text{ kg})(5 times 10^6text{ m/s})}{(1.602 times 10^{-19}text{ C})(1.5text{ T})} approx 0.0348text{ m}[/latex]
Thus, the proton would move in a circle with a radius of approximately 3.48 cm.
5. What Are Some Real-World Applications?
The principles of charged particle motion in uniform magnetic fields are applied in numerous technologies and scientific instruments.
Mass Spectrometry
Mass spectrometry uses magnetic fields to determine the mass-to-charge ratio of ions.
- Ionization: Molecules are ionized to create charged particles.
- Acceleration: Ions are accelerated through an electric field.
- Magnetic Field: Ions pass through a magnetic field, causing them to move in a circular path.
- Detection: The radius of the path is measured to determine the mass-to-charge ratio.
Particle Accelerators
Particle accelerators use magnetic fields to guide and accelerate charged particles to high speeds.
- Magnetic Confinement: Magnetic fields keep particles in a circular path.
- Acceleration: Electric fields accelerate particles to high energies.
- Collision: Particles collide to study fundamental physics.
Magnetic Resonance Imaging (MRI)
MRI uses strong magnetic fields and radio waves to create detailed images of the human body.
- Magnetic Field Alignment: Protons in the body align with a strong magnetic field.
- Radio Waves: Radio waves disrupt the alignment, causing protons to emit signals.
- Image Creation: Signals are processed to create detailed images of tissues and organs.
Plasma Confinement in Fusion Reactors
Uniform magnetic fields are used to confine plasma in fusion reactors.
- High Temperature: Plasma is heated to extremely high temperatures.
- Magnetic Confinement: Magnetic fields prevent the plasma from touching the reactor walls.
- Fusion: Plasma is compressed to initiate nuclear fusion reactions.
6. How Do Magnetic Bottles Work?
Magnetic bottles trap charged particles using non-uniform magnetic fields. Particles move along spiral paths, reflecting between regions of high magnetic field strength.
Understanding Magnetic Bottles
Magnetic bottles rely on the principle that charged particles moving into stronger magnetic fields experience a force pushing them back towards the weaker field.
- Non-Uniform Field: The magnetic field is stronger at the ends of the bottle.
- Reflection: Particles spiral along field lines, reflecting at the strong field regions.
- Trapping: Particles are trapped between the reflection points.
Applications of Magnetic Bottles
Magnetic bottles have significant applications in various fields.
- Plasma Confinement: Used in fusion research to confine high-temperature plasma.
- Van Allen Belts: Earth’s magnetic field forms natural magnetic bottles, trapping charged particles.
- Particle Storage: Used in experiments to store and study charged particles.
The Van Allen Belts
The Van Allen radiation belts are regions around Earth where charged particles are trapped by Earth’s magnetic field.
- Discovery: Discovered by James Van Allen in 1958.
- Particle Source: Particles originate from solar wind and cosmic rays.
- Belt Structure: Consist of an inner and outer belt, with varying particle energies.
- Aurorae: Interactions between trapped particles and the atmosphere cause auroras.
7. What Is the Relationship Between Magnetic Fields and Aurorae?
Aurorae, such as the Aurora Borealis (Northern Lights) and Aurora Australis (Southern Lights), are caused by charged particles interacting with Earth’s atmosphere along magnetic field lines.
The Science Behind Aurorae
Aurorae are a spectacular display of light caused by the collision of charged particles with atmospheric gases.
- Solar Wind: Charged particles from the sun travel to Earth.
- Magnetic Field Interaction: Earth’s magnetic field guides particles to the polar regions.
- Atmospheric Collision: Particles collide with oxygen and nitrogen atoms in the atmosphere.
- Light Emission: Collisions excite atoms, causing them to emit light of various colors.
Colors of Aurorae
The colors of aurorae depend on the type of gas and the altitude of the collision.
| Color | Gas | Altitude (km) |
|---|---|---|
| Green | Oxygen | 100-200 |
| Red | Oxygen | Above 200 |
| Blue | Nitrogen | 100-200 |
| Purple | Nitrogen | Below 100 |
Observing Aurorae
Aurorae are best observed in high-latitude regions during periods of high solar activity.
- Location: Alaska, Canada, Scandinavia, and Antarctica.
- Timing: During geomagnetic storms and solar flares.
- Visibility: Clear, dark skies away from light pollution.
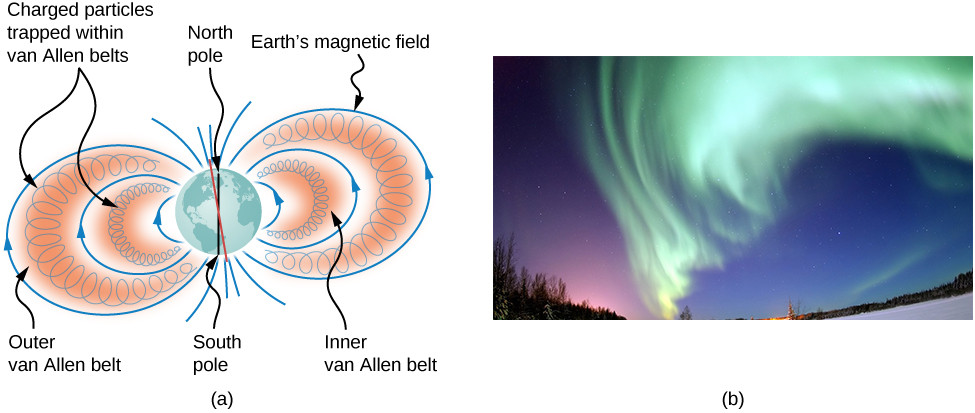 Aurora Borealis, showcasing the interaction between charged particles and Earth's atmosphere
Aurora Borealis, showcasing the interaction between charged particles and Earth's atmosphere
8. How Is the Beam Deflector Used?
A beam deflector uses a magnetic field to change the direction of a beam of charged particles. This is crucial in applications such as particle therapy and isotope separation.
Working Principle of a Beam Deflector
The beam deflector works by applying a magnetic force on charged particles, causing them to deviate from their original path.
- Uniform Magnetic Field: A uniform magnetic field is applied over a specific region.
- Charged Particles: A beam of charged particles enters the magnetic field.
- Deflection: The magnetic force deflects the particles, changing their direction.
- Controlled Trajectory: By adjusting the magnetic field, the deflection angle can be controlled.
Applications of Beam Deflectors
Beam deflectors are essential in various scientific and industrial applications.
- Particle Therapy: Directing beams of protons or ions to target cancerous tumors.
- Isotope Separation: Separating isotopes based on their mass-to-charge ratio.
- Mass Spectrometry: Controlling the path of ions in mass spectrometers.
- Research: Used in physics experiments to manipulate particle beams.
Example: Alpha Particle Deflector
Consider an alpha particle ([latex]m = 6.64 times 10^{-27}[/latex] kg, [latex]q = 3.2 times 10^{-19}[/latex] C) moving through a magnetic field of 0.050 T. To calculate the time it takes for the alpha particle to traverse a 90-degree bend, we use the formula:
[latex]T = frac{2pi m}{qB}[/latex]
[latex]T = frac{2pi (6.64 times 10^{-27}text{ kg})}{(3.2 times 10^{-19}text{ C})(0.050text{ T})} approx 2.6 times 10^{-6}text{ s}[/latex]
Since the particle is only going through a quarter circle (90 degrees), the time taken is:
[latex]t = 0.25 times 2.6 times 10^{-6}text{ s} approx 6.5 times 10^{-7}text{ s}[/latex]
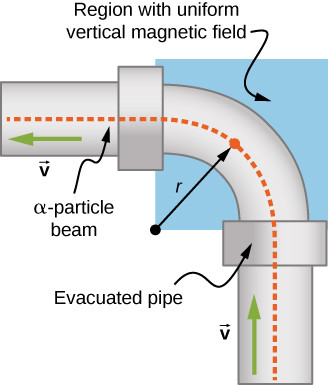 Beam deflector setup illustrating the path of alpha particles through a magnetic field
Beam deflector setup illustrating the path of alpha particles through a magnetic field
9. How Do You Calculate Helical Motion in a Magnetic Field?
Calculating helical motion involves determining the radius and pitch of the helix, which depend on the particle’s velocity components parallel and perpendicular to the magnetic field.
Steps to Calculate Helical Motion
- Determine Velocity Components:
- [latex]v_{parallel} = v cos theta[/latex] (parallel component)
- [latex]v_{perp} = v sin theta[/latex] (perpendicular component)
- Calculate Radius (r):
- [latex]r = frac{mv_{perp}}{qB}[/latex]
- Calculate Period (T):
- [latex]T = frac{2pi m}{qB}[/latex]
- Calculate Pitch (p):
- [latex]p = v_{parallel} T[/latex]
Example Calculation
Consider a proton ([latex]m = 1.672 times 10^{-27}[/latex] kg, [latex]q = 1.602 times 10^{-19}[/latex] C) entering a magnetic field of [latex]1.0 times 10^{-4}[/latex] T at a speed of [latex]5 times 10^5[/latex] m/s and an angle of 81 degrees.
- Velocity Components:
- [latex]v_{parallel} = (5 times 10^5text{ m/s}) cos(81^circ) approx 7.81 times 10^4text{ m/s}[/latex]
- [latex]v_{perp} = (5 times 10^5text{ m/s}) sin(81^circ) approx 4.92 times 10^5text{ m/s}[/latex]
- Radius:
- [latex]r = frac{(1.672 times 10^{-27}text{ kg})(4.92 times 10^5text{ m/s})}{(1.602 times 10^{-19}text{ C})(1.0 times 10^{-4}text{ T})} approx 0.0513text{ m}[/latex]
- Period:
- [latex]T = frac{2pi (1.672 times 10^{-27}text{ kg})}{(1.602 times 10^{-19}text{ C})(1.0 times 10^{-4}text{ T})} approx 6.56 times 10^{-4}text{ s}[/latex]
- Pitch:
- [latex]p = (7.81 times 10^4text{ m/s})(6.56 times 10^{-4}text{ s}) approx 0.0513text{ m}[/latex]
Thus, the proton moves in a helix with a radius of approximately 5.13 cm and a pitch of approximately 5.13 cm.
10. What Are Some Common Misconceptions About Magnetic Fields?
Several misconceptions exist regarding magnetic fields and their effects on charged particles.
Common Misconceptions
- Magnetic Fields Exert Force on All Charges:
- Reality: Magnetic fields only exert force on moving charges. A stationary charge experiences no magnetic force.
- Magnetic Force Changes Particle Speed:
- Reality: Magnetic force changes the direction of the particle’s velocity but not its speed. The force is always perpendicular to the velocity, doing no work.
- Uniform Magnetic Field Means No Force:
- Reality: A uniform magnetic field exerts a constant force on a moving charge, causing it to move in a circular or helical path.
- Magnetic Fields Only Exist Near Magnets:
- Reality: Magnetic fields are also produced by moving electric charges, such as in electric currents and electromagnetic waves.
Clarifying Misconceptions
Understanding the true nature of magnetic fields requires dispelling these common misconceptions.
- Force on Moving Charges: Magnetic force [latex]vec{F} = q(vec{v} times vec{B})[/latex] depends on the charge [latex]q[/latex] and velocity [latex]vec{v}[/latex] of the particle and the magnetic field [latex]vec{B}[/latex].
- Work Done by Magnetic Force: Magnetic force does no work on the charged particle, as the force is always perpendicular to the displacement.
- Sources of Magnetic Fields: Magnetic fields are created by permanent magnets and moving electric charges.
Conclusion
Understanding the behavior of charged particles in uniform magnetic fields is crucial for various applications, from mass spectrometry and particle accelerators to MRI and plasma confinement. By grasping the fundamental principles and dispelling common misconceptions, we can better appreciate the role of magnetic fields in science and technology.
At onlineuniforms.net, we understand the importance of quality and reliability. Whether you’re in the medical field, education, or any other industry requiring professional attire, we’ve got you covered.
Ready to elevate your team’s appearance with custom uniforms? Visit onlineuniforms.net today to explore our extensive collection and customization options! Contact us at +1 (214) 651-8600 or visit our location at 1515 Commerce St, Dallas, TX 75201, United States.
FAQ: Uniform Magnetic Fields
-
What is a uniform magnetic field?
A uniform magnetic field is perpendicular is a region where the magnetic field strength and direction are the same at every point. This is crucial for many applications.
-
How does a charged particle move in a uniform magnetic field?
A charged particle moves in a circular or helical path in a uniform magnetic field, depending on its initial velocity relative to the field.
-
What factors affect the radius of circular motion?
The radius of circular motion depends on the particle’s mass, velocity, charge, and the strength of the magnetic field.
-
What is helical motion?
Helical motion is the combination of circular motion and linear motion along the magnetic field lines.
-
What is a magnetic bottle?
A magnetic bottle is a region of non-uniform magnetic field used to trap charged particles.
-
How are magnetic fields used in mass spectrometry?
Magnetic fields are used in mass spectrometry to separate ions based on their mass-to-charge ratio.
-
What causes aurorae?
Aurorae are caused by charged particles from the sun interacting with Earth’s atmosphere along magnetic field lines.
-
How does a beam deflector work?
A beam deflector uses a magnetic field to change the direction of a beam of charged particles.
-
What is the Van Allen radiation belt?
The Van Allen radiation belts are regions around Earth where charged particles are trapped by Earth’s magnetic field.
-
What are some misconceptions about magnetic fields?
Common misconceptions include the belief that magnetic fields exert force on all charges and that magnetic force changes particle speed.
