How To Find Uniform Charge Density From Sigma?

Finding uniform charge density from sigma is key to understanding electromagnetism. Let’s explore how you can determine this relationship and apply it practically, especially when considering uniform needs for your business or organization, with solutions available at onlineuniforms.net.

1. What Is Uniform Charge Density and Why Does It Matter?

Uniform charge density refers to the amount of electric charge per unit length, area, or volume, when the charge is evenly distributed. Understanding it is fundamental in electromagnetism for calculating electric fields and potentials. For example, the Uniform Manufacturers and Distributors Association (UMDA) highlighted in July 2025 the importance of understanding material densities for creating effective electromagnetic shielding.

Key Takeaways:

• It’s a measure of how much electric charge is in a specific space.
• Crucial for calculating electric fields.
• Essential in applications like capacitor design and electromagnetic shielding.

1.1. Types of Charge Density

There are three primary types:

• Linear Charge Density (λ): Charge per unit length (C/m).
• Surface Charge Density (σ): Charge per unit area (C/m²).
• Volume Charge Density (ρ): Charge per unit volume (C/m³).

1.2. Relevance in Electromagnetism

Charge density is used to calculate electric fields using integral calculus. The electric field (E) at a point due to a continuous charge distribution is given by:

• For a line charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{line}} left(dfrac{lambda , dl}{r^2}right) hat{r} ])
• For a surface charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{surface}} left(dfrac{sigma ,dA}{r^2}right) hat{r} ])
• For a volume charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{volume}} left(dfrac{rho ,dV}{r^2}right) hat{r} ])

1.3. Application in Uniforms

While directly applying charge density to uniforms might seem abstract, understanding material properties and distributions can be useful. For instance, in designing uniforms with specific electrostatic properties for sensitive environments (like cleanrooms), charge distribution knowledge is critical.

2. What Is Sigma (σ) and Its Significance?

Sigma (σ) represents surface charge density, measuring electric charge per unit area, and is vital for analyzing surface charge distributions in materials.

Key Points:

• Definition: Electric charge per unit area (C/m²).
• Importance: Critical in understanding the behavior of charged surfaces.
• Applications: Essential in capacitor design, semiconductor physics, and materials science.

2.1. Surface Charge Density Explained

Surface charge density describes how electric charge is distributed across a surface. It is typically denoted by the Greek letter sigma (σ) and is measured in coulombs per square meter (C/m²).

2.2. Why Sigma Matters

• Capacitors: In capacitors, sigma determines the amount of charge stored on the plates, affecting the capacitance and energy storage capabilities.
• Semiconductors: In semiconductor devices, surface charge density influences the behavior of transistors and other components.
• Electrostatic Shielding: Understanding sigma helps in designing effective shields against electromagnetic interference.

2.3. Using Sigma in Calculations

Given the surface charge density σ, the total charge Q on a surface A is:

(Q = int sigma , dA)

If σ is uniform (constant), the equation simplifies to:

(Q = sigma A)

2.4. Sigma in Real-World Applications

• Touchscreens: The operation of touchscreens depends on the surface charge distribution on the screen.
• Photocopiers: Surface charge density plays a role in the toner transfer process in photocopiers.
• Electrostatic Painting: In electrostatic painting, the uniformity of the paint coating is influenced by the surface charge density.

3. How Are Uniform Charge Density and Sigma Related?

When dealing with a uniformly charged surface, the uniform charge density is numerically equal to sigma (σ). This simplifies calculations, as the charge is evenly distributed.

3.1. Defining Uniform Charge Density

Uniform charge density means that the charge is evenly distributed across a given dimension (length, area, or volume). Mathematically:

• Linear: λ = Q/L (where L is the length).
• Surface: σ = Q/A (where A is the area).
• Volume: ρ = Q/V (where V is the volume).

3.2. The Connection

In a uniform surface charge distribution, sigma (σ) directly represents the uniform charge density. Thus, if you know the total charge Q and the area A over which it is distributed, you can find sigma as:

(sigma = frac{Q}{A})

3.3. Implications of Uniformity

When the charge density is uniform, calculations become simpler. For instance, the electric field due to a uniformly charged disk can be calculated using:

([vec{E}(z) = dfrac{1}{4 pi epsilon_0} left( 2 pi sigma – dfrac{2 pi sigma z}{sqrt{R^2 + z^2}}right)hat{k}. ])

Where:

• z is the distance from the disk.
• R is the radius of the disk.

3.4. Practical Examples

• Capacitor Plates: Ideal parallel-plate capacitors assume a uniform surface charge density on their plates.
• Conducting Spheres: A conducting sphere in electrostatic equilibrium has a uniform surface charge density if no external fields are present.

4. Step-By-Step Guide to Finding Uniform Charge Density From Sigma

To find uniform charge density from sigma, follow these steps: Identify the surface, determine the total charge, measure the surface area, and then calculate sigma (σ = Q/A).

4.1. Step 1: Identify the Surface

• Define the Surface: Determine the geometry of the surface over which the charge is distributed (e.g., disk, sphere, plane).
• Example: A circular disk with radius R.

4.2. Step 2: Determine the Total Charge (Q)

• Measure or Calculate Q: Find the total electric charge Q distributed on the surface.
• Units: Coulombs (C).

4.3. Step 3: Measure the Surface Area (A)

• Calculate A: Use the appropriate formula to find the surface area A.
• Formulas:
  • Disk: (A = pi R^2)
  • Sphere: (A = 4 pi R^2)
  • Rectangle: (A = lw) (length * width)

4.4. Step 4: Calculate Sigma (σ)

• Apply the Formula: Divide the total charge Q by the surface area A to find sigma (σ).
• Formula: (sigma = frac{Q}{A})
• Units: Coulombs per square meter (C/m²)

4.5. Example Calculation

Problem: A circular disk of radius 0.1 m has a total charge of 5 × 10⁻⁶ C uniformly distributed on its surface. Find the surface charge density σ.

Solution:

1. Surface: Circular disk.
2. Total Charge: (Q = 5 times 10^{-6} , textrm{C})
3. Surface Area: (A = pi R^2 = pi (0.1 , textrm{m})^2 approx 0.0314 , textrm{m}^2)
4. Sigma: (sigma = frac{Q}{A} = frac{5 times 10^{-6} , textrm{C}}{0.0314 , textrm{m}^2} approx 1.59 times 10^{-4} , textrm{C/m}^2)

4.6. Important Considerations

• Units: Ensure all units are consistent (SI units are recommended).
• Uniformity: The charge distribution must be uniform for this method to be accurate.
• Precision: Use appropriate significant figures in your calculations.

5. Formulas and Equations for Calculating Charge Density

Understanding the formulas for calculating linear, surface, and volume charge densities is critical for various applications in electromagnetism.

5.1. Linear Charge Density (λ)

• Definition: Charge per unit length.
• Formula:
  (lambda = frac{Q}{L})
  where:
  • λ is the linear charge density (C/m)
  • Q is the total charge (C)
  • L is the length (m)

5.2. Surface Charge Density (σ)

• Definition: Charge per unit area.
• Formula:
  (sigma = frac{Q}{A})
  where:
  • σ is the surface charge density (C/m²)
  • Q is the total charge (C)
  • A is the area (m²)

5.3. Volume Charge Density (ρ)

• Definition: Charge per unit volume.
• Formula:
  (rho = frac{Q}{V})
  where:
  • ρ is the volume charge density (C/m³)
  • Q is the total charge (C)
  • V is the volume (m³)

5.4. Key Equations for Electric Field Calculation

The electric field E due to different charge distributions can be calculated using the following equations:

• Line Charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{line}} left(dfrac{lambda , dl}{r^2}right) hat{r} ])
• Surface Charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{surface}} left(dfrac{sigma ,dA}{r^2}right) hat{r} ])
• Volume Charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{volume}} left(dfrac{rho ,dV}{r^2}right) hat{r} ])

5.5. Practical Application: Electric Field of an Infinite Plane

The electric field due to an infinite plane with uniform surface charge density σ is:

([ begin{align} vec{E} &= lim_{R rightarrow infty} dfrac{1}{4 pi epsilon_0} left( 2 pi sigma – dfrac{2 pi sigma z}{sqrt{R^2 + z^2}}right)hat{k} \[4pt] &= dfrac{sigma}{2 epsilon_0} hat{k}. label{5.15} end{align} ])

Where:

• (epsilon_0) is the permittivity of free space (approximately (8.854 times 10^{-12} , textrm{C}^2/textrm{N}cdottextrm{m}^2)).

5.6. Example Calculation: Uniformly Charged Sphere

Consider a sphere of radius R with a total charge Q uniformly distributed throughout its volume. The volume charge density ρ is:

(rho = frac{Q}{V} = frac{Q}{frac{4}{3} pi R^3})

The electric field outside the sphere (at a distance r > R) is the same as that of a point charge:

(E = frac{1}{4 pi epsilon_0} frac{Q}{r^2})

6. Examples of Uniform Charge Density in Different Geometries

Understanding how uniform charge density applies to different geometries is crucial for solving electromagnetism problems.

6.1. Line Charge

• Geometry: Infinitely long, thin wire.
• Charge Distribution: Uniformly distributed along the wire.
• Linear Charge Density: (lambda = frac{Q}{L})
• Electric Field: The electric field at a distance r from the wire is:
  (E = frac{lambda}{2 pi epsilon_0 r})

6.2. Surface Charge (Disk)

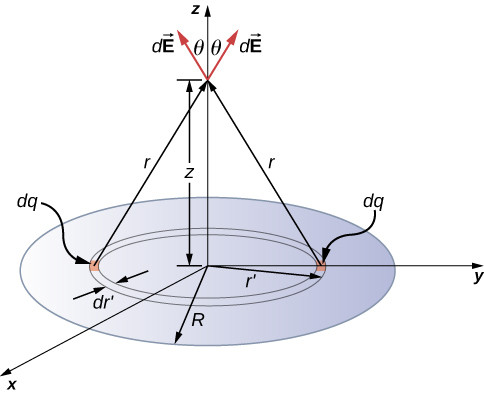A uniformly charged disk. As in the line charge example, the field above the center of this disk can be calculated by taking advantage of the symmetry of the charge distribution.

• Geometry: Thin, circular disk.
• Charge Distribution: Uniformly distributed on the surface.
• Surface Charge Density: (sigma = frac{Q}{A} = frac{Q}{pi R^2})
• Electric Field: The electric field at a distance z above the center of the disk is:
  ([vec{E}(z) = dfrac{1}{4 pi epsilon_0} left( 2 pi sigma – dfrac{2 pi sigma z}{sqrt{R^2 + z^2}}right)hat{k}. ])

6.3. Infinite Plane

The figure shows two vertically oriented parallel plates A and B separated by a distance d. Plate A is positively charged and B is negatively charged. Electric field lines are parallel between the plates and curved outward at the ends of the plates. A charge q is moved from A to B. The work done W equals q times V sub A B, and the electric field intensity E equals V sub A B over d.

• Geometry: Infinitely large, flat sheet.
• Charge Distribution: Uniformly distributed on the surface.
• Surface Charge Density: (sigma = frac{Q}{A})
• Electric Field: The electric field at any point near the plane is:
  (E = frac{sigma}{2 epsilon_0})

6.4. Sphere

• Geometry: Solid sphere.
• Charge Distribution: Uniformly distributed throughout the volume.
• Volume Charge Density: (rho = frac{Q}{V} = frac{Q}{frac{4}{3} pi R^3})
• Electric Field:
  • Outside the sphere (r > R): (E = frac{1}{4 pi epsilon_0} frac{Q}{r^2})
  • Inside the sphere (r < R): (E = frac{rho r}{3 epsilon_0})

6.5. Practical Implications

• Capacitors: Understanding uniform charge distributions helps in designing and analyzing capacitors.
• Electrostatic Shielding: Knowledge of charge densities is crucial for creating effective shields against electromagnetic interference.
• Material Science: Surface charge density influences the behavior of materials in various applications.

7. Common Mistakes to Avoid When Calculating Charge Density

Accurate calculations of charge density are crucial in electromagnetism, and avoiding common mistakes can save time and prevent errors.

7.1. Incorrect Units

• Mistake: Using mixed or incorrect units for charge, length, area, or volume.
• Solution: Always use SI units:
  • Charge (Q): Coulombs (C)
  • Length (L): Meters (m)
  • Area (A): Square meters (m²)
  • Volume (V): Cubic meters (m³)

7.2. Assuming Uniformity Incorrectly

• Mistake: Assuming the charge distribution is uniform when it is not.
• Solution: Verify the charge distribution before applying formulas for uniform charge density. If the distribution is non-uniform, use integration to find the total charge.

7.3. Incorrectly Calculating Area or Volume

• Mistake: Using the wrong formula for the area or volume of the geometry involved.
• Solution: Use the correct formulas for calculating area and volume:
  • Sphere: (A = 4 pi R^2), (V = frac{4}{3} pi R^3)
  • Disk: (A = pi R^2)
  • Cylinder: (A = 2 pi r h), (V = pi r^2 h)

7.4. Forgetting Constants

• Mistake: Forgetting to include constants like the permittivity of free space ((epsilon_0)) in electric field calculations.
• Solution: Always include all relevant constants in your calculations.

7.5. Sign Errors

• Mistake: Making errors with the sign of the charge.
• Solution: Pay careful attention to the sign of the charge, as it affects the direction of the electric field.

7.6. Overlooking Symmetry

• Mistake: Failing to use symmetry to simplify calculations.
• Solution: Look for symmetries in the charge distribution to simplify the integral expressions for electric fields.

7.7. Misunderstanding the Question

• Mistake: Not fully understanding what the question is asking.
• Solution: Read the problem carefully and identify what you are trying to find.

7.8. Examples of Mistakes and Corrections

• Mistake: Calculating the surface charge density on a sphere using (A = pi R^2) instead of (A = 4 pi R^2).
• Correction: Use the correct formula (A = 4 pi R^2) for the surface area of a sphere.
• Mistake: Assuming uniform charge density on a conductor with an irregular shape.
• Correction: Recognize that charge will accumulate at points of high curvature on the conductor, so the charge density is not uniform.

8. Advanced Concepts: Non-Uniform Charge Density

While uniform charge density provides a simplified model, many real-world scenarios involve non-uniform charge distributions. Understanding these advanced concepts is essential for more complex applications.

8.1. What Is Non-Uniform Charge Density?

• Definition: Charge density that varies with position. The charge is not evenly distributed across the length, area, or volume.

8.2. Mathematical Representation

Non-uniform charge density is represented as a function of position:

• (lambda(x)) for linear charge density.
• (sigma(x, y)) for surface charge density.
• (rho(x, y, z)) for volume charge density.

8.3. Calculating Total Charge

To find the total charge Q in a non-uniform distribution, integrate the charge density over the appropriate dimension:

• Linear: (Q = int lambda(x) , dx)
• Surface: (Q = int int sigma(x, y) , dA)
• Volume: (Q = int int int rho(x, y, z) , dV)

8.4. Calculating Electric Fields

The electric field due to a non-uniform charge distribution is calculated using similar integrals, but with the variable charge density:

• Line Charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{line}} left(dfrac{lambda(x) , dx}{r^2}right) hat{r} ])
• Surface Charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{surface}} left(dfrac{sigma(x, y) ,dA}{r^2}right) hat{r} ])
• Volume Charge:
  ([ vec{E}(P) = dfrac{1}{4pi epsilon_0} int_{textrm{volume}} left(dfrac{rho(x, y, z) ,dV}{r^2}right) hat{r} ])

8.5. Examples of Non-Uniform Charge Distributions

• Charge Near a Point: The charge density near a sharp point on a conductor is higher than on flatter surfaces.
• Atmospheric Charge: The charge density in the Earth’s atmosphere varies with altitude.
• Semiconductor Doping: The doping concentration in semiconductors varies spatially to create electronic devices.

8.6. Applications

• High-Voltage Engineering: Understanding non-uniform charge distributions is critical for designing high-voltage equipment to avoid breakdown.
• Medical Imaging: Charge distributions in the human body during medical imaging are non-uniform.
• Nanotechnology: The behavior of nanomaterials often depends on non-uniform charge distributions.

8.7. Techniques for Solving Non-Uniform Problems

• Numerical Methods: Use computational techniques like the Finite Element Method (FEM) to solve complex problems.
• Approximations: Use approximations and simplifications to make the problem tractable.

9. Tools and Resources for Calculating Charge Density

Several tools and resources can aid in calculating charge density, ranging from online calculators to advanced simulation software.

9.1. Online Calculators

• Charge Density Calculators: Websites that offer calculators for linear, surface, and volume charge density.
• Electric Field Calculators: Tools for calculating the electric field due to various charge distributions.

9.2. Simulation Software

• COMSOL Multiphysics: A powerful simulation tool for modeling electromagnetic fields and charge distributions.
• ANSYS: Widely used for simulating electromagnetic fields and analyzing charge density in complex geometries.
• MATLAB: Can be used to write custom scripts for calculating charge density and electric fields.

9.3. Textbooks and Academic Resources

• University Physics Textbooks: Standard physics textbooks provide comprehensive coverage of electromagnetism and charge density calculations.
• Online Courses: Platforms like Coursera, edX, and MIT OpenCourseWare offer courses on electromagnetism and related topics.

9.4. Websites and Forums

• Physics Forums: Online communities where you can ask questions and get help with physics problems.
• Stack Exchange (Physics): A question-and-answer website for physicists.

9.5. Open-Source Tools

• Python Libraries: Libraries like NumPy and SciPy can be used for numerical calculations and simulations.

9.6. Tips for Using Resources Effectively

• Verify Results: Always double-check your results using multiple methods or tools.
• Understand Limitations: Be aware of the limitations of the tools you are using.
• Consult Experts: Don’t hesitate to ask for help from experts or colleagues.

9.7. Example: Using COMSOL for Charge Density Calculation

1. Set Up Geometry: Create a model of the geometry in COMSOL.
2. Define Material Properties: Assign material properties such as permittivity.
3. Apply Charge Distribution: Specify the charge distribution (uniform or non-uniform).
4. Solve: Run the simulation to calculate the charge density and electric field.
5. Visualize Results: Use COMSOL’s visualization tools to examine the charge density distribution.

10. Charge Density in Real-World Applications

Charge density concepts are essential in numerous real-world applications, from electronics to environmental science.

10.1. Capacitors

• Application: Energy storage.
• Role of Charge Density: The amount of charge stored on the capacitor plates is directly related to the surface charge density.

10.2. Semiconductors

• Application: Transistors, diodes, and integrated circuits.
• Role of Charge Density: The behavior of semiconductor devices depends on the charge density of doped regions.

10.3. Electrostatic Shielding

• Application: Protecting electronic equipment from electromagnetic interference.
• Role of Charge Density: Designing effective shields requires understanding how charge distributes on the shielding material.

10.4. Electrostatic Painting

• Application: Applying paint evenly to surfaces.
• Role of Charge Density: The uniformity of the paint coating depends on the charge density of the paint particles.

10.5. Medical Imaging

• Application: MRI and CT scans.
• Role of Charge Density: Understanding charge distributions in the human body is essential for accurate imaging.

10.6. Environmental Science

• Application: Studying atmospheric electricity.
• Role of Charge Density: The distribution of charge in the atmosphere affects weather patterns and lightning strikes.

10.7. Cleanroom Technology

• Application: Maintaining particle-free environments.
• Role of Charge Density: Controlling electrostatic discharge (ESD) by managing charge accumulation on surfaces.

10.8. Nanotechnology

• Application: Designing nanoscale devices.
• Role of Charge Density: Charge distribution plays a critical role in the behavior of nanomaterials and devices.

10.9. Examples

• Touchscreens: The operation of touchscreens depends on the surface charge distribution on the screen.
• Photocopiers: Surface charge density plays a role in the toner transfer process in photocopiers.
• Laser Printers: Charge density guides the toner particles to the drum to create images and text.

FAQ: Frequently Asked Questions About Finding Uniform Charge Density

1. How Do I Know If a Charge Distribution Is Uniform?

A charge distribution is uniform if the charge is evenly distributed across the given length, area, or volume. Mathematically, the charge density (λ, σ, or ρ) is constant.

2. What Is the Difference Between Linear, Surface, and Volume Charge Density?

• Linear Charge Density (λ): Charge per unit length (C/m).
• Surface Charge Density (σ): Charge per unit area (C/m²).
• Volume Charge Density (ρ): Charge per unit volume (C/m³).

3. How Is Sigma (σ) Related to the Electric Field?

Sigma (σ) is used to calculate the electric field due to a surface charge distribution. The electric field at a point near a surface with charge density σ is:

(E = frac{sigma}{2 epsilon_0})

4. What Are the Units for Charge Density?

• Linear: C/m
• Surface: C/m²
• Volume: C/m³

5. Can Charge Density Be Negative?

Yes, charge density can be negative, indicating a negative charge distribution.

6. How Do I Calculate the Total Charge From the Charge Density?

• Linear: (Q = int lambda , dl)
• Surface: (Q = int sigma , dA)
• Volume: (Q = int rho , dV)

7. What If the Charge Density Is Not Uniform?

If the charge density is not uniform, you must use integration to calculate the total charge and electric field.

8. Where Can I Find Values for the Permittivity of Free Space (ε₀)?

The permittivity of free space (ε₀) is approximately (8.854 × 10⁻¹² C²/N·m²).

9. What Are Some Common Geometries Used in Charge Density Problems?

• Line Charge
• Disk
• Infinite Plane
• Sphere

10. How Does Charge Density Relate to Uniforms?

While not directly related, understanding charge density helps in designing specialized uniforms with desired electrostatic properties, such as those used in cleanrooms.

Understanding “How To Find Uniform Charge Density From Sigma” is crucial for mastering electromagnetism, from basic calculations to advanced applications. If you are interested in high-quality uniforms, visit onlineuniforms.net, Address: 1515 Commerce St, Dallas, TX 75201, United States. Phone: +1 (214) 651-8600. Visit onlineuniforms.net today to explore options, request a quote, and get expert advice.