Is Angular Velocity Constant In Uniform Circular Motion? Yes, angular velocity is constant in uniform circular motion; onlineuniforms.net provides uniforms tailored for various professions, ensuring comfort and style for those engaged in physics or any field. Our collection supports the blend of theoretical understanding and practical application, offering a professional appearance and durable wear for your daily needs, enhancing your understanding and engagement with the world of physics. Discover our durable workwear and enhance your professional image with onlineuniforms.net.
1. Understanding Uniform Circular Motion
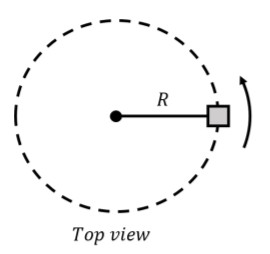
Uniform circular motion describes an object moving along a circular path at a constant speed. The object’s speed remains constant, the direction of its velocity continuously changes, and it is always tangent to the circular path.
1.1 What Defines Uniform Circular Motion?
Several key characteristics define uniform circular motion:
- Constant Speed: The object moves at a steady pace around the circle.
- Changing Velocity: Although the speed is constant, the velocity changes because direction changes constantly.
- Centripetal Acceleration: Acceleration is always directed toward the center of the circle, ensuring the object remains on its circular path.
These characteristics underscore the fundamental principles governing this type of motion.
1.2 Visualizing Uniform Circular Motion
Imagine a car moving around a circular track at a constant speed. The car’s speedometer remains steady, but the car’s direction constantly changes, necessitating continuous adjustment by the driver. This simple example illustrates the basic concept of uniform circular motion.
2. Angular Velocity: A Deep Dive
Angular velocity measures how quickly an object rotates or revolves relative to a particular point. It’s a vector quantity, meaning it has both magnitude and direction.
2.1 Definition of Angular Velocity
Angular velocity ((ω)) is defined as the rate of change of angular displacement. It’s typically measured in radians per second (rad/s). The formula for angular velocity is:
[
ω = frac{Δθ}{Δt}
]
Where:
- (Δθ) is the change in angular displacement (in radians)
- (Δt) is the change in time (in seconds)
2.2 Factors Influencing Angular Velocity
Several factors can affect angular velocity:
- Torque: Applying a torque (rotational force) will change the angular velocity.
- Moment of Inertia: An object’s resistance to changes in its rotational motion.
- External Forces: Forces that impact the object’s rotation.
However, in uniform circular motion, these factors are carefully balanced to maintain a constant angular velocity.
2.3 Alt Text: A spinning carousel in an amusement park, illustrating uniform circular motion.
A spinning carousel in an amusement park, illustrating uniform circular motion.
3. Is Angular Velocity Constant?
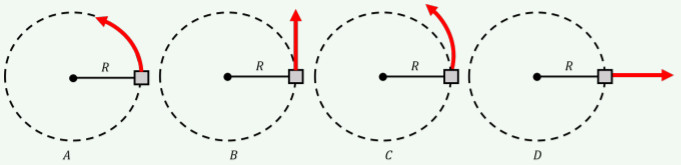
Yes, angular velocity is constant in uniform circular motion. The object covers equal angles in equal intervals of time.
3.1 Constant Speed and Constant Angular Velocity
In uniform circular motion, constant speed directly implies constant angular velocity. Since the radius of the circular path does not change, the rate at which the object sweeps through angles remains constant.
The relationship between linear speed ((v)) and angular velocity ((ω)) is given by:
[
v = ωr
]
Where:
- (v) is the linear speed
- (ω) is the angular velocity
- (r) is the radius of the circular path
Since (v) and (r) are constant in uniform circular motion, (ω) must also be constant.
3.2 Zero Angular Acceleration
Another way to confirm that angular velocity is constant is by noting that angular acceleration ((α)) is zero in uniform circular motion. Angular acceleration is the rate of change of angular velocity:
[
α = frac{Δω}{Δt}
]
If (ω) is constant, then (Δω = 0), which means (α = 0).
3.3 Real-World Examples
Consider these real-world examples to illustrate constant angular velocity:
- A fan spinning at a constant rate: Each blade covers the same angle in the same amount of time.
- A CD spinning in a CD player: The CD rotates at a constant angular velocity to ensure consistent playback.
- A turntable spinning at a set speed: Vinyl records rotate at a constant rate to maintain the correct pitch and tempo of the music.
4. Mathematical Proof
To mathematically prove that angular velocity is constant, we start with the basic equations of circular motion.
4.1 Derivation from Basic Equations
In uniform circular motion, the angular displacement ((θ)) changes linearly with time:
[
θ = ωt + θ_0
]
Where:
- (θ) is the angular displacement at time (t)
- (ω) is the angular velocity
- (t) is the time
- (θ_0) is the initial angular displacement
Differentiating both sides with respect to time, we get:
[
frac{dθ}{dt} = ω
]
This confirms that the angular velocity ((ω)) is constant since it does not depend on time.
4.2 Applying Calculus
Using calculus provides a more rigorous proof. The position vector ( vec{r}(t) ) of an object in uniform circular motion can be described as:
[
vec{r}(t) = R cos(ωt) hat{i} + R sin(ωt) hat{j}
]
Where:
- (R) is the radius of the circle
- (ω) is the angular velocity
- (hat{i}) and (hat{j}) are the unit vectors in the x and y directions, respectively
The velocity vector ( vec{v}(t) ) is the derivative of the position vector with respect to time:
[
vec{v}(t) = frac{dvec{r}(t)}{dt} = -Rω sin(ωt) hat{i} + Rω cos(ωt) hat{j}
]
The speed ( v(t) ) is the magnitude of the velocity vector:
[
v(t) = sqrt{(-Rω sin(ωt))^2 + (Rω cos(ωt))^2} = Rω
]
Since ( R ) is constant and ( v(t) ) is constant in uniform circular motion, ( ω ) must also be constant.
5. Implications of Constant Angular Velocity
The constancy of angular velocity has several important implications in physics and engineering.
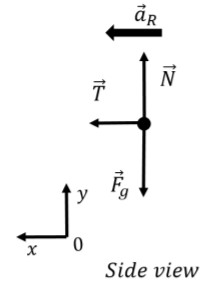
5.1 Centripetal Acceleration
In uniform circular motion, the centripetal acceleration ((a_c)) is given by:
[
a_c = frac{v^2}{r} = ω^2r
]
Since (ω) and (r) are constant, the magnitude of the centripetal acceleration is also constant. This acceleration is always directed toward the center of the circle, continuously changing the direction of the velocity vector to keep the object moving along the circular path.
5.2 Kinetic Energy
The rotational kinetic energy ((KE_{rot})) of an object in uniform circular motion is given by:
[
KE_{rot} = frac{1}{2}Iω^2
]
Where (I) is the moment of inertia. Since (ω) is constant, the rotational kinetic energy remains constant as well, provided the moment of inertia does not change.
5.3 Alt Text: A runner on a circular track, showcasing constant angular velocity and the relationship between linear and angular motion.
A runner on a circular track, showcasing constant angular velocity and the relationship between linear and angular motion.
6. Uniform Circular Motion vs. Non-Uniform Circular Motion
It’s essential to distinguish between uniform and non-uniform circular motion to fully understand the role of angular velocity.
6.1 Key Differences
The main difference lies in the constancy of speed and angular velocity:
- Uniform Circular Motion: Constant speed and constant angular velocity.
- Non-Uniform Circular Motion: Changing speed and changing angular velocity.
6.2 Examples of Non-Uniform Circular Motion
Examples of non-uniform circular motion include:
- A roller coaster loop: The speed varies as the coaster goes around the loop.
- A spinning top slowing down: Friction causes the angular velocity to decrease.
- A car accelerating around a curve: The car’s speed increases, leading to changing angular velocity.
6.3 Equations for Non-Uniform Circular Motion
In non-uniform circular motion, angular acceleration ((α)) is not zero. The equations of motion become:
[
ω = ω_0 + αt
]
[
θ = ω_0t + frac{1}{2}αt^2
]
[
ω^2 = ω_0^2 + 2αθ
]
Where (ω_0) is the initial angular velocity.
7. Applications in Various Fields
Understanding uniform circular motion and constant angular velocity is crucial in many fields.
7.1 Engineering
In mechanical engineering, understanding circular motion is essential for designing rotating machinery, such as turbines, engines, and gears. Ensuring components move with constant angular velocity is vital for efficiency and reliability.
7.2 Physics
In physics, uniform circular motion is a fundamental concept for understanding more complex motions and forces. It’s a building block for understanding rotational dynamics and celestial mechanics.
7.3 Astronomy
In astronomy, the motion of planets around stars can be approximated as uniform circular motion in certain scenarios. This helps in predicting planetary positions and understanding orbital mechanics.
7.4 Alt Text: A Ferris wheel in motion, exemplifying circular motion principles in engineering design.
A Ferris wheel in motion, exemplifying circular motion principles in engineering design.
8. Common Misconceptions
Several misconceptions often arise when learning about uniform circular motion.
8.1 Velocity vs. Speed
A common mistake is thinking that constant speed implies constant velocity. While the speed is constant, the velocity changes because its direction changes continuously.
8.2 Centripetal Force
Another misconception is that centripetal force is a “real” force acting on the object. Centripetal force is the net force that causes the object to move in a circle; it’s not a separate, distinct force.
8.3 Inertial Forces
Many people confuse centripetal force with centrifugal force. Centrifugal force is an apparent force that arises in a non-inertial (rotating) frame of reference. It is not a real force acting on the object from an external source.
9. Advanced Topics
For those interested in delving deeper, several advanced topics build upon the principles of uniform circular motion.
9.1 Coriolis Effect
The Coriolis effect is an apparent deflection of moving objects when viewed from a rotating reference frame. This effect is significant in meteorology and oceanography, influencing wind patterns and ocean currents.
9.2 Foucault Pendulum
The Foucault pendulum demonstrates the Earth’s rotation. The pendulum’s plane of oscillation rotates over time due to the Coriolis effect, providing visual evidence of Earth’s rotation.
9.3 Rotational Dynamics
Rotational dynamics involves the study of torques, moments of inertia, and angular momentum. It provides a more comprehensive understanding of rotational motion and its causes.
10. Practical Examples and Exercises
To reinforce understanding, let’s explore some practical examples and exercises.
10.1 Example 1: Calculating Angular Velocity
A wheel with a radius of 0.5 meters completes one revolution in 2 seconds. Calculate its angular velocity.
Solution:
One revolution is (2π) radians. The time taken is 2 seconds. Therefore, the angular velocity is:
[
ω = frac{2π}{2} = π approx 3.14 text{ rad/s}
]
10.2 Example 2: Finding Centripetal Acceleration
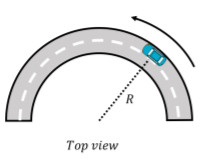
A car is moving around a circular track with a radius of 100 meters at a constant speed of 20 m/s. Calculate the centripetal acceleration.
Solution:
The centripetal acceleration is given by:
[
a_c = frac{v^2}{r} = frac{(20)^2}{100} = 4 text{ m/s}^2
]
10.3 Exercise 1
A merry-go-round completes 5 revolutions in 10 seconds. Calculate its angular velocity.
10.4 Exercise 2
A satellite orbits the Earth in a circular path with a radius of 7000 km at a constant speed of 7500 m/s. Calculate its centripetal acceleration.
11. How onlineuniforms.net Supports Professionals
At onlineuniforms.net, we understand the importance of professionalism and comfort in various fields. Our uniforms are designed to meet the specific needs of professionals across different industries.
11.1 High-Quality Materials
We use only the highest quality materials to ensure durability and comfort. Our fabrics are selected to withstand the demands of daily wear while providing a professional appearance.
11.2 Customization Options
We offer a range of customization options, including embroidery and logo placement, to help businesses and organizations create a cohesive and professional image.
11.3 Wide Range of Industries
Our selection includes uniforms for medical professionals, educators, and various other sectors. Each uniform is designed to meet the unique requirements of the job.
11.4 Alt Text: A group of medical professionals in onlineuniforms.net uniforms, showcasing professionalism and comfort.
A group of medical professionals in onlineuniforms.net uniforms, showcasing professionalism and comfort.
12. Conclusion
In summary, angular velocity is indeed constant in uniform circular motion, which is a fundamental concept with broad applications across various fields. A solid grasp of uniform circular motion enables deeper insights into physics and engineering. Whether you’re a physics enthusiast or a professional requiring high-quality uniforms, understanding these concepts enhances your appreciation and expertise. For reliable and comfortable uniforms tailored to your profession, visit onlineuniforms.net today and discover our wide range of options.
13. Frequently Asked Questions (FAQs)
-
What is uniform circular motion?
Uniform circular motion is the motion of an object moving at a constant speed along a circular path. -
Is the velocity constant in uniform circular motion?
No, the velocity is not constant because the direction of motion continuously changes, even though the speed is constant. -
What is angular velocity?
Angular velocity is the rate at which an object rotates or revolves relative to a point, measured in radians per second (rad/s). -
Is angular velocity constant in uniform circular motion?
Yes, angular velocity is constant in uniform circular motion because the object covers equal angles in equal intervals of time. -
What is centripetal acceleration?
Centripetal acceleration is the acceleration directed toward the center of the circle, which keeps the object moving along its circular path. -
What is the relationship between linear speed and angular velocity?
The relationship is given by the formula (v = ωr), where (v) is linear speed, (ω) is angular velocity, and (r) is the radius of the circular path. -
What is angular acceleration in uniform circular motion?
Angular acceleration is zero in uniform circular motion because the angular velocity is constant. -
What is non-uniform circular motion?
Non-uniform circular motion occurs when an object moves along a circular path with changing speed and angular velocity. -
What are some examples of non-uniform circular motion?
Examples include a roller coaster loop, a spinning top slowing down, and a car accelerating around a curve. -
How does onlineuniforms.net support professionals?
onlineuniforms.net supports professionals by providing high-quality, customizable uniforms designed for various industries, ensuring comfort, durability, and a professional appearance.
Ready to explore high-quality uniforms tailored to your profession? Visit onlineuniforms.net to view our wide range of options, request a quote, and contact us for personalized assistance. Our address is 1515 Commerce St, Dallas, TX 75201, United States. You can reach us by phone at +1 (214) 651-8600. Enhance your professional image with onlineuniforms.net today!
