In statistics, the uniform distribution, sometimes also known as the rectangular distribution, is a type of probability distribution where every possible outcome within a certain range is equally likely. This distribution is defined by two parameters, (a) and (b), which are the minimum and maximum values of the range respectively. Understanding the properties of a uniform distribution, such as its standard deviation, is crucial in various fields including probability theory, statistics, and data analysis.
Let’s explore the uniform distribution through a practical example. Consider Ace Heating and Air Conditioning Service, where the repair time for a furnace is uniformly distributed between 1.5 and 4 hours. We can represent this as (x sim U(1.5, 4)), where (x) is the time needed to fix a furnace. In this article, we will delve into calculating probabilities, percentiles, and importantly, the standard deviation of this uniform distribution.
Calculating Probabilities with Uniform Distribution
For a uniform distribution (U(a, b)), the probability density function (PDF) is constant over the interval ([a, b]) and zero elsewhere. The height of this constant function, (f(x)), is given by (frac{1}{b-a}). For our furnace repair example, (a = 1.5) and (b = 4), so the height of the PDF is:
[f(x) = frac{1}{4 – 1.5} = frac{1}{2.5} = 0.4]
This means for any value (x) between 1.5 and 4, the probability density is 0.4. To find the probability of an event within this uniform distribution, we calculate the area under the PDF curve within the specified range.
Probability of Repair Time Exceeding Two Hours
Let’s calculate the probability that a randomly selected furnace repair takes more than two hours. We need to find (P(x > 2)). This probability is represented by the area of the rectangle with base ((4 – 2)) and height (0.4).
[P(x > 2) = (text{base}) times (text{height}) = (4 – 2) times 0.4 = 2 times 0.4 = 0.8]
Therefore, there is an 80% chance that a furnace repair will take more than two hours.
Uniform Distribution between 1.5 and four with shaded area between two and four representing the probability that the repair time x is greater than two
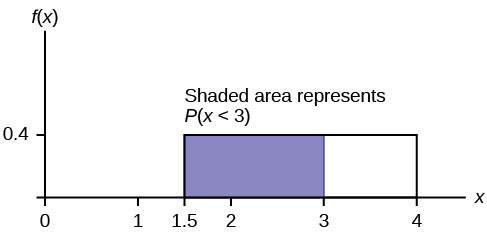
Probability of Repair Time Being Less Than Three Hours
Now, let’s find the probability that a repair takes less than three hours, (P(x < 3)). This is the area under the PDF from (x = 1.5) (the lower bound) to (x = 3). The base of this rectangle is ((3 – 1.5)) and the height is still (0.4).
[P(x < 3) = (text{base}) times (text{height}) = (3 – 1.5) times 0.4 = 1.5 times 0.4 = 0.6]
So, there is a 60% probability that a furnace repair will require less than three hours.
Uniform Distribution between 1.5 and four with shaded area between two and four representing the probability that the repair time x is greater than two
Percentiles in Uniform Distribution
Percentiles divide a dataset into 100 parts. The 30th percentile, for example, is the value below which 30% of the data falls. For a uniform distribution, finding percentiles involves determining the value (k) such that the area to the left of (k) under the PDF is equal to the desired percentile.
Finding the 30th Percentile
To find the 30th percentile of furnace repair times, we need to find (k) such that (P(x < k) = 0.30). This corresponds to the area of a rectangle with height (0.4) and base ((k – 1.5)).
[0.30 = (k – 1.5) times 0.4]
Solving for (k):
[frac{0.30}{0.4} = k – 1.5]
[0.75 = k – 1.5]
[k = 0.75 + 1.5 = 2.25]
Thus, the 30th percentile of furnace repair times is 2.25 hours. This means 30% of repair times are 2.25 hours or less.
Uniform Distribution between 1.5 and four with shaded area between two and four representing the probability that the repair time x is greater than two
Determining the Time for the Longest 25% of Repairs (75th Percentile)
We want to find the minimum time for the longest 25% of repair times. This is equivalent to finding the value (k) such that (P(x > k) = 0.25). This also means we are looking for the 75th percentile, as 75% of the repair times are less than or equal to this value.
[P(x > k) = (4 – k) times 0.4 = 0.25]
Solving for (k):
[frac{0.25}{0.4} = 4 – k]
[0.625 = 4 – k]
[k = 4 – 0.625 = 3.375]
The longest 25% of furnace repairs take at least 3.375 hours. Therefore, 3.375 hours represents the 75th percentile of furnace repair times.
Mean and Standard Deviation of the Uniform Distribution
For a uniform distribution (U(a, b)), the mean ((mu)) and standard deviation ((sigma)) are given by simple formulas:
Mean:
[mu = frac{a + b}{2}]
Standard Deviation:
[sigma = sqrt{frac{(b – a)^2}{12}}]
The mean represents the average value of the distribution, which for a uniform distribution is simply the midpoint of the interval ([a, b]). The standard deviation measures the spread or dispersion of the distribution. A higher standard deviation indicates a wider spread of values.
Calculating Mean and Standard Deviation for Furnace Repair Times
For our furnace repair example, (a = 1.5) and (b = 4). Let’s calculate the mean and standard deviation.
Mean:
[mu = frac{1.5 + 4}{2} = frac{5.5}{2} = 2.75]
The mean repair time is 2.75 hours.
Standard Deviation:
[sigma = sqrt{frac{(4 – 1.5)^2}{12}} = sqrt{frac{(2.5)^2}{12}} = sqrt{frac{6.25}{12}} approx sqrt{0.5208} approx 0.7217]
The standard deviation of the furnace repair times is approximately 0.7217 hours. This value tells us about the variability in repair times around the mean. A standard deviation of 0.7217 hours indicates a moderate spread of repair times around the average of 2.75 hours, which is a key characteristic of the Standard Deviation Of The Uniform Distribution.
Conclusion
Understanding the uniform distribution and its properties, especially the standard deviation, is essential for analyzing data where outcomes are evenly distributed within a range. The standard deviation provides a measure of the spread of the distribution, complementing the mean which indicates the central tendency. By using simple formulas, we can easily calculate these key measures and apply them to practical problems, such as estimating probabilities and percentiles in scenarios like furnace repair times, providing valuable insights into the data’s behavior and variability.
