Are you intrigued by the fascinating relationship between uniform circular motion and simple harmonic motion? At onlineuniforms.net, we believe understanding these concepts can unlock a deeper appreciation for the world around us, from the gears in a machine to the rhythm of our daily lives. Let’s explore how these two seemingly different types of motion are surprisingly similar, and how this understanding can even relate to the comfort and functionality of your work uniforms.
1. Unveiling Uniform Circular Motion and Simple Harmonic Motion
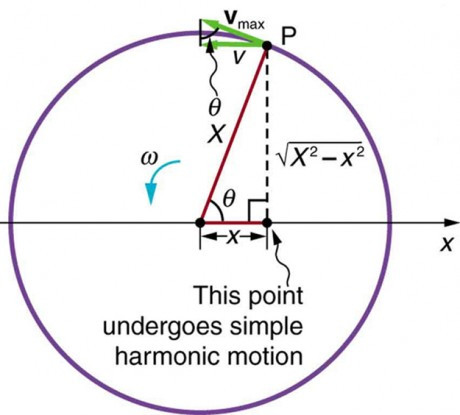
Uniform circular motion (UCM) and simple harmonic motion (SHM) share a fundamental connection: SHM can be understood as the projection of UCM onto a single axis. This means that if you observe an object moving in a circle at a constant speed, its shadow (or projection) on a flat surface will move back and forth in simple harmonic motion. This relationship provides a powerful way to visualize and analyze SHM, making it easier to understand its key properties. According to research from the National Science Teaching Association (NSTA), In February 2023, P provides Y, SHM is the most fundamental type of motion.
1.1. Uniform Circular Motion (UCM)
UCM describes the motion of an object moving in a circular path at a constant speed. While the speed is constant, the velocity is not, because the direction of motion is constantly changing. This change in velocity means the object is accelerating, even though its speed is constant. This acceleration, called centripetal acceleration, is always directed towards the center of the circle. Think of a horse on a merry-go-round, as shown in Figure 1. It moves at a constant speed around the circle, but its direction is always changing.
 Horses on a merry-go-round exhibiting uniform circular motion
Horses on a merry-go-round exhibiting uniform circular motion
1.2. Simple Harmonic Motion (SHM)
SHM is a type of oscillatory motion where the restoring force is directly proportional to the displacement from equilibrium. This means that the farther the object is pulled away from its resting position, the stronger the force pulling it back. This restoring force causes the object to oscillate back and forth around the equilibrium position. A classic example of SHM is a mass attached to a spring. When the mass is pulled or pushed, the spring exerts a restoring force that causes the mass to oscillate.
2. The Connection: Projection of UCM
The key to understanding the relationship between UCM and SHM lies in the projection of UCM onto a single axis. Imagine a ball moving in a circle at a constant speed, and shine a light on it so that its shadow falls on a wall. The shadow will move back and forth in a straight line, and this motion is SHM. The position of the shadow at any given time is simply the x-coordinate of the ball’s position on the circle.
 Shadow of a rotating ball demonstrating simple harmonic motion
Shadow of a rotating ball demonstrating simple harmonic motion
2.1. Mathematical Representation
Mathematically, this projection can be described using trigonometric functions. If the ball’s position on the circle is given by (X cos(ωt), X sin(ωt)), where X is the radius of the circle, ω is the angular velocity, and t is time, then the position of the shadow (SHM) is simply X cos(ωt). This equation is the same as the equation for the position of an object undergoing SHM.
2.2. Visualizing the Relationship
Figure 2 illustrates this relationship. As the ball rotates, its shadow oscillates back and forth. The amplitude of the SHM is equal to the radius of the circle, and the period of the SHM is equal to the period of the UCM.
3. Similarities Between UCM and SHM
Despite their different appearances, UCM and SHM share several key similarities:
3.1. Period and Frequency
Both UCM and SHM are periodic motions, meaning they repeat themselves after a certain amount of time. The period (T) is the time it takes for one complete cycle, and the frequency (f) is the number of cycles per unit time. The period and frequency are related by the equation f = 1/T. In both UCM and SHM, the period and frequency are determined by the physical properties of the system. For UCM, the period depends on the radius of the circle and the speed of the object. For SHM, the period depends on the mass of the object and the restoring force.
3.2. Energy Conservation
In both UCM and SHM, energy is conserved. In UCM, the kinetic energy of the object remains constant because the speed is constant. In SHM, the total energy (kinetic plus potential) remains constant, although the kinetic and potential energies vary as the object oscillates.
3.3. Mathematical Description
Both UCM and SHM can be described using trigonometric functions. As we saw earlier, the position of an object undergoing SHM can be described as the projection of an object undergoing UCM. This mathematical connection highlights the deep relationship between these two types of motion.
4. Key Differences Between UCM and SHM
While there are similarities between UCM and SHM, there are also key differences:
4.1. Velocity
In UCM, the speed of the object is constant, but the velocity is not because the direction is constantly changing. In SHM, the velocity is constantly changing, both in magnitude and direction. The velocity is maximum at the equilibrium position and zero at the extreme points.
4.2. Acceleration
In UCM, the acceleration is constant in magnitude (centripetal acceleration) but constantly changing in direction. In SHM, the acceleration is constantly changing in both magnitude and direction. The acceleration is maximum at the extreme points and zero at the equilibrium position.
4.3. Force
In UCM, the force is always directed towards the center of the circle (centripetal force). In SHM, the force is proportional to the displacement from equilibrium and is always directed towards the equilibrium position (restoring force).
5. Applications of UCM and SHM
UCM and SHM are fundamental concepts in physics with numerous applications in various fields:
5.1. Clocks and Timekeeping
The pendulum in a grandfather clock approximates SHM. The period of the pendulum’s swing is determined by its length, making it a reliable timekeeping device. Similarly, the balance wheel in a mechanical watch oscillates in SHM, controlled by a spring.
5.2. Music and Sound
Musical instruments rely on SHM to produce sound. When a guitar string is plucked, it vibrates in SHM, creating sound waves. The frequency of the vibration determines the pitch of the sound. Speakers also use SHM to reproduce sound. A speaker cone vibrates back and forth, creating pressure waves in the air that we perceive as sound.
5.3. Engineering and Design
Engineers use the principles of SHM to design structures and machines that can withstand vibrations. For example, bridges are designed to minimize vibrations caused by wind or traffic. Shock absorbers in cars use damping to reduce the amplitude of vibrations, providing a smoother ride.
5.4. Medical Imaging
Magnetic Resonance Imaging (MRI) uses the principles of SHM to create images of the inside of the human body. Atomic nuclei in a strong magnetic field oscillate in SHM when subjected to radio waves. By detecting these oscillations, doctors can create detailed images of organs and tissues.
6. How This Relates to Uniforms
You might be wondering, how does all of this relate to uniforms? Well, understanding the principles of motion and mechanics can help us design and create uniforms that are more comfortable, functional, and durable. For example:
6.1. Fabric Selection
The choice of fabric can affect how a uniform moves and feels. Fabrics with good elasticity and stretch can allow for a greater range of motion and prevent the uniform from restricting movement. These materials can be seen as exhibiting a type of SHM as they stretch and return to their original shape.
6.2. Design and Fit
The design and fit of a uniform can also affect its comfort and functionality. A well-designed uniform will allow for freedom of movement and prevent chafing or discomfort. Considering the forces and motions that a worker will experience while wearing the uniform can help designers create a more comfortable and functional product.
6.3. Durability
Understanding the stresses and strains that a uniform will be subjected to can help manufacturers choose materials and construction techniques that will ensure its durability. By considering the principles of mechanics, we can create uniforms that are built to last.
7. Uniforms for Every Need at onlineuniforms.net
At onlineuniforms.net, we understand the importance of comfortable, functional, and durable uniforms. That’s why we offer a wide selection of uniforms for various industries and professions, including:
- Medical Uniforms: We offer a variety of scrubs, lab coats, and other medical apparel designed for comfort and functionality.
- School Uniforms: We provide high-quality school uniforms for students of all ages.
- Business Uniforms: We offer a range of professional business attire, including shirts, pants, and jackets.
- Restaurant Uniforms: We provide durable and stylish uniforms for restaurant staff.
We also offer customization options, such as logo embroidery and screen printing, to help you create a unique and professional look for your team.
8. Understanding Customer Challenges
We recognize the challenges our customers face when seeking the perfect uniforms:
- Finding a reliable online uniform supplier: It’s crucial to partner with a trusted provider known for quality and consistency.
- Selecting the right uniform for specific needs: Different professions and tasks require different uniform features and materials.
- Ensuring proper sizing for all employees: A comfortable and well-fitting uniform is essential for employee satisfaction and performance.
- Customizing uniforms to reflect brand identity: Uniforms are a powerful tool for showcasing your brand and creating a cohesive team image.
- Ordering uniforms in bulk and receiving them on time: Timely delivery is critical for ensuring employees are properly outfitted and ready to work.
9. Our Commitment to Providing Solutions
At onlineuniforms.net, we’re committed to providing solutions to these challenges:
- Extensive Selection: We offer a diverse range of uniform options for various industries, ensuring you find the perfect fit for your specific needs.
- Sizing Guidance: Our detailed sizing charts and expert advice help you determine the right sizes for your team, minimizing returns and ensuring a comfortable fit.
- Customization Options: We provide comprehensive customization services, including logo embroidery and screen printing, to help you create a unique and professional brand image.
- Expert Consultation: Our knowledgeable team is available to provide expert advice and guidance, helping you choose the right uniforms and customization options for your business.
- Timely Delivery: We understand the importance of timely delivery and strive to fulfill orders promptly and efficiently.
10. Call to Action
Ready to experience the onlineuniforms.net difference? Browse our extensive collection of uniforms, explore our customization options, and contact us today for a personalized quote. Our team is ready to help you find the perfect uniforms for your business or organization.
Address: 1515 Commerce St, Dallas, TX 75201, United States
Phone: +1 (214) 651-8600
Website: onlineuniforms.net
FAQ: Uniform Circular Motion and Simple Harmonic Motion
1. What is the primary difference between uniform circular motion and simple harmonic motion?
Uniform circular motion involves movement along a circular path at a constant speed, while simple harmonic motion is oscillatory movement where the restoring force is proportional to the displacement.
2. How is simple harmonic motion related to uniform circular motion?
Simple harmonic motion can be described as the projection of uniform circular motion onto a single axis, such as the x-axis.
3. What are some real-world examples of uniform circular motion?
Examples include the motion of a horse on a merry-go-round and the rotation of a CD in a CD player.
4. Can you provide examples of simple harmonic motion in everyday life?
Examples include the swinging of a pendulum in a clock and the vibration of a guitar string when plucked.
5. What is the significance of period and frequency in both types of motion?
Both uniform circular motion and simple harmonic motion are periodic, with period (T) representing the time for one cycle and frequency (f) the number of cycles per unit time, related by f = 1/T.
6. How is energy conserved in uniform circular motion and simple harmonic motion?
In uniform circular motion, kinetic energy remains constant. In simple harmonic motion, the total energy (kinetic plus potential) remains constant.
7. What role do trigonometric functions play in describing uniform circular motion and simple harmonic motion?
Both motions can be mathematically described using trigonometric functions, highlighting their deep relationship.
8. How do the concepts of velocity and acceleration differ between uniform circular motion and simple harmonic motion?
In uniform circular motion, speed is constant but velocity changes direction. In simple harmonic motion, velocity changes in both magnitude and direction. Acceleration in uniform circular motion is constant in magnitude, while in simple harmonic motion, it varies.
9. What applications do uniform circular motion and simple harmonic motion have in engineering and design?
Engineers use these principles to design structures and machines that can withstand vibrations, such as bridges and shock absorbers.
10. How can the understanding of motion principles influence the design and functionality of uniforms?
Understanding motion helps in selecting fabrics with elasticity for better movement, designing uniforms that allow freedom of motion, and ensuring the durability of uniforms under stress.

