Is Uniform Circular Motion Uniformly Accelerated Motion?

Uniform circular motion, often encountered in various physical scenarios, involves an object moving at a constant speed along a circular path; onlineuniforms.net provides information and resources on practical applications of physics concepts. Understanding whether this motion qualifies as uniformly accelerated is crucial, as it influences the design and functionality of many mechanical systems, from the uniforms worn by professionals in these fields to the equipment they use. This exploration will clarify the nature of uniform circular motion and its relationship to acceleration, providing you with a clear understanding.

1. Understanding Uniform Circular Motion

Uniform circular motion describes the movement of an object traveling at a constant speed along a circular path. This type of motion is characterized by a consistent radius and a fixed rate of rotation.

1.1. Key Characteristics

Constant Speed: The object’s speed remains the same throughout its circular trajectory.
Fixed Radius: The distance from the object to the center of the circle is constant.
Continuous Direction Change: Although the speed is constant, the object’s velocity continuously changes direction.

1.2. Real-World Examples

Satellites in Orbit: Many satellites maintain a nearly uniform circular orbit around the Earth.
Rotating Machinery: Components in machines like fans and turbines often exhibit uniform circular motion.
Cars on Circular Tracks: When a car moves around a circular track at a constant speed, it undergoes uniform circular motion.

2. Acceleration in Uniform Circular Motion

Acceleration is defined as the rate of change of velocity. In uniform circular motion, even though the speed is constant, the direction of the velocity is continuously changing. This change in direction implies that the object is indeed accelerating.

2.1. Centripetal Acceleration

The acceleration experienced by an object in uniform circular motion is known as centripetal acceleration (ac). This acceleration is always directed towards the center of the circle and is responsible for keeping the object moving along the circular path.

The magnitude of centripetal acceleration is given by:

$$ a_c = frac{v^2}{r} $$

Where:

( a_c ) is the centripetal acceleration.
( v ) is the speed of the object.
( r ) is the radius of the circular path.

Centripetal Acceleration Formula

2.2. Direction of Acceleration

The key characteristic of centripetal acceleration is that its direction is always changing. At any point on the circular path, the acceleration vector points directly towards the center of the circle. This continuous change in direction distinguishes it from uniform acceleration, where both magnitude and direction remain constant.

3. Is It Uniformly Accelerated Motion?

To determine if uniform circular motion is uniformly accelerated, we must analyze whether both the magnitude and direction of the acceleration remain constant.

3.1. Magnitude of Acceleration

In uniform circular motion, the magnitude of the centripetal acceleration ( a_c = frac{v^2}{r} ) is constant because both the speed ( v ) and the radius ( r ) are constant.

3.2. Direction of Acceleration

However, the direction of the centripetal acceleration is not constant. It continuously changes to point towards the center of the circle. This continuous change in direction means that the acceleration is not uniform.

3.3. Conclusion

Therefore, uniform circular motion is not uniformly accelerated motion because the direction of the acceleration vector is constantly changing, even though its magnitude remains constant.

4. Comparing Uniform Circular Motion and Uniformly Accelerated Motion

To further clarify the distinction, let’s compare uniform circular motion with uniformly accelerated motion (also known as constant acceleration).

4.1. Uniformly Accelerated Motion

Definition: Motion in which the acceleration is constant in both magnitude and direction.
Examples:
1. Free Fall: An object falling under the influence of gravity experiences constant acceleration downwards.
2. Object Sliding on an Inclined Plane: If the plane is frictionless, the object accelerates at a constant rate.
3. Car Accelerating in a Straight Line: If a car increases its speed at a steady rate, it undergoes uniformly accelerated motion.

4.2. Key Differences

Feature	Uniform Circular Motion	Uniformly Accelerated Motion
Path	Circular	Straight Line
Speed	Constant	Changing
Velocity	Changing direction	Changing magnitude (and direction if in a straight line)
Acceleration	Constant magnitude, changing direction (towards the center)	Constant magnitude and direction
Type of Acceleration	Centripetal	Linear
Examples	Satellite orbiting at constant speed, rotating fan at fixed rate	Free fall, car accelerating at a constant rate on a straight road

5. Mathematical Analysis of Centripetal Acceleration

To understand centripetal acceleration more deeply, let’s delve into its mathematical derivation and implications.

5.1. Derivation of Centripetal Acceleration

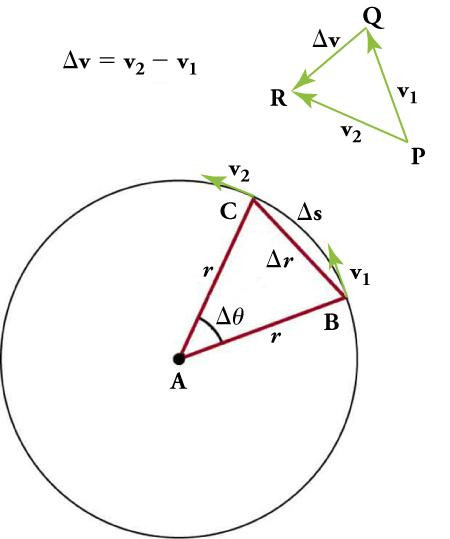
Consider an object moving in a circle of radius ( r ) with a constant speed ( v ). At time ( t ), the object is at point ( A ) and at time ( t + Delta t ), it is at point ( B ).

Position Vectors: Let ( vec{r_1} ) and ( vec{r_2} ) be the position vectors at points ( A ) and ( B ) respectively.
Velocity Vectors: Let ( vec{v_1} ) and ( vec{v_2} ) be the velocity vectors at points ( A ) and ( B ) respectively.

Since the speed is constant, ( |vec{v_1}| = |vec{v_2}| = v ). The change in velocity ( Delta vec{v} ) is given by:

$$ Delta vec{v} = vec{v_2} – vec{v_1} $$

The average acceleration ( vec{a_{avg}} ) is:

$$ vec{a_{avg}} = frac{Delta vec{v}}{Delta t} $$

As ( Delta t ) approaches zero, ( vec{a_{avg}} ) becomes the instantaneous acceleration ( vec{a} ), which is directed towards the center of the circle. The magnitude of this acceleration is:

$$ a = lim_{Delta t to 0} frac{|Delta vec{v}|}{Delta t} = frac{v^2}{r} $$

This confirms that the magnitude of centripetal acceleration is ( frac{v^2}{r} ) and its direction is always towards the center.

5.2. Angular Velocity and Centripetal Acceleration

Centripetal acceleration can also be expressed in terms of angular velocity ( omega ), which is the rate at which the object rotates around the circle (measured in radians per second). The relationship between linear velocity ( v ) and angular velocity ( omega ) is:

$$ v = romega $$

Substituting this into the centripetal acceleration formula:

$$ a_c = frac{(romega)^2}{r} = romega^2 $$

Thus, the centripetal acceleration can also be expressed as ( a_c = romega^2 ).

6. Practical Applications and Implications

Understanding uniform circular motion and centripetal acceleration is vital in numerous fields, impacting engineering designs, safety considerations, and technological advancements.

6.1. Engineering Design

Road and Track Design: Civil engineers use the principles of centripetal acceleration when designing curved roads and racetracks. Banking the curves (creating a slope) helps to provide the necessary centripetal force, reducing the reliance on friction and making it safer for vehicles to navigate the curve at higher speeds.
Rotating Machinery: Mechanical engineers consider centripetal acceleration in the design of rotating machinery such as turbines, centrifuges, and fans. Ensuring that components can withstand the forces due to centripetal acceleration is critical for the reliability and safety of these machines.
Aerospace Engineering: In aerospace engineering, understanding centripetal acceleration is essential for designing aircraft maneuvers and satellite orbits. Calculating the required centripetal force ensures that spacecraft maintain their intended paths.

6.2. Safety Considerations

Vehicle Safety: Automotive engineers use the concept of centripetal acceleration to design safety systems such as anti-lock braking systems (ABS) and electronic stability control (ESC). These systems help drivers maintain control when turning, especially on slippery surfaces, by preventing the wheels from locking up and losing traction.
Amusement Park Rides: Designers of amusement park rides, such as roller coasters and Ferris wheels, carefully calculate centripetal forces to ensure the safety and enjoyment of riders.

6.3. Technological Advancements

Centrifuges: Centrifuges, used in medical and scientific laboratories, employ centripetal acceleration to separate substances based on density. By spinning samples at high speeds, heavier particles are forced to the bottom of the tube, allowing for separation and analysis.
Gyroscopes: Gyroscopes, used in navigation systems and inertial measurement units (IMUs), rely on the principles of centripetal acceleration to maintain orientation and stability. They are used in aircraft, ships, and spacecraft to provide accurate directional information.

7. Centripetal Force and Its Role

Centripetal force is the force that causes an object to move in a circular path. It is always directed toward the center of the circle and is essential for maintaining uniform circular motion.

7.1. Source of Centripetal Force

The centripetal force is not a fundamental force of nature but rather a net force that can be provided by various sources, depending on the situation.

Tension: In the case of an object tied to a string and swung in a circle, the tension in the string provides the centripetal force.
Gravity: For satellites orbiting a planet, the gravitational force between the satellite and the planet provides the centripetal force.
Friction: When a car turns on a flat road, the friction between the tires and the road provides the centripetal force.
Normal Force: On a banked curve, a component of the normal force exerted by the road on the car provides the centripetal force.

7.2. Mathematical Representation

The magnitude of the centripetal force ( F_c ) can be calculated using Newton’s second law:

$$ F_c = ma_c $$

Since ( a_c = frac{v^2}{r} ), the centripetal force can also be written as:

$$ F_c = frac{mv^2}{r} $$

Where:

( F_c ) is the centripetal force.
( m ) is the mass of the object.
( v ) is the speed of the object.
( r ) is the radius of the circular path.

7.3. Examples of Centripetal Force

Swinging a Ball on a String: When you swing a ball attached to a string in a horizontal circle, the tension in the string provides the centripetal force that keeps the ball moving in a circular path. If the string breaks, the ball will fly off in a straight line tangent to the circle, illustrating Newton’s first law.
Earth Orbiting the Sun: The Earth orbits the Sun due to the gravitational force between them. This gravitational force acts as the centripetal force, constantly pulling the Earth toward the Sun and keeping it in its orbit.
Car Turning a Corner: When a car turns a corner, the friction between the tires and the road provides the centripetal force. On a flat road, this friction is the only force preventing the car from skidding outwards. Banking the road helps by providing a component of the normal force to assist with the centripetal force, reducing the reliance on friction.

8. Advanced Concepts Related to Circular Motion

Beyond the basics of uniform circular motion, there are several advanced concepts that build upon these principles and are essential for a comprehensive understanding.

8.1. Non-Uniform Circular Motion

Non-uniform circular motion occurs when an object moves along a circular path with a changing speed. In this case, the object experiences both centripetal acceleration (due to the change in direction) and tangential acceleration (due to the change in speed).

Tangential Acceleration: Tangential acceleration ( a_t ) is the component of acceleration that is tangent to the circular path. It is responsible for changing the speed of the object.
Total Acceleration: The total acceleration ( a ) in non-uniform circular motion is the vector sum of the centripetal acceleration ( a_c ) and the tangential acceleration ( a_t ):

$$ vec{a} = vec{a_c} + vec{a_t} $$

The magnitude of the total acceleration is:

$$ a = sqrt{a_c^2 + a_t^2} $$

8.2. Coriolis Effect

The Coriolis effect is an apparent deflection of moving objects when viewed from a rotating reference frame. It is significant in meteorology, oceanography, and astronomy.

Explanation: The Coriolis effect is not a real force but rather an effect of inertia in a rotating system. Objects moving in a straight line appear to curve when viewed from a rotating frame of reference.
Impact on Weather: In meteorology, the Coriolis effect causes moving air masses to deflect to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. This deflection influences the formation of weather patterns, such as cyclones and trade winds.

8.3. Moment of Inertia

Moment of inertia is a measure of an object’s resistance to rotational motion about an axis. It depends on the mass of the object and the distribution of mass relative to the axis of rotation.

Definition: The moment of inertia ( I ) is defined as:

$$ I = sum m_i r_i^2 $$

Where ( m_i ) is the mass of each particle in the object and ( r_i ) is the distance of each particle from the axis of rotation.

Relationship to Angular Acceleration: The moment of inertia is analogous to mass in linear motion and relates torque ( tau ) to angular acceleration ( alpha ) by:

$$ tau = Ialpha $$

8.4. Angular Momentum

Angular momentum is a measure of the amount of rotation an object has, taking into account its mass, velocity, and shape. It is a conserved quantity, meaning that in a closed system, the total angular momentum remains constant unless acted upon by an external torque.

Definition: Angular momentum ( L ) is defined as:

$$L = Iomega$$

Where ( I ) is the moment of inertia and ( omega ) is the angular velocity.
Conservation of Angular Momentum: In the absence of external torques, angular momentum is conserved:

$$I_1omega_1 = I_2omega_2$$

This principle is demonstrated by figure skaters, who can increase their rotational speed by pulling their arms closer to their body, decreasing their moment of inertia and thus increasing their angular velocity.

9. Common Misconceptions About Circular Motion

Understanding circular motion can be challenging, and there are several common misconceptions that students and others often have.

9.1. Centrifugal Force is a Real Force

Misconception: Centrifugal force is often thought to be a real force pulling objects outward in circular motion.

Clarification: Centrifugal force is a fictitious force or pseudo-force. It is not a real force in the same way that gravity or electromagnetism are. Instead, it is the effect of inertia experienced in a non-inertial (rotating) reference frame. In an inertial frame of reference, the only real force acting on the object is the centripetal force, which pulls the object toward the center of the circle.

9.2. Constant Speed Means No Acceleration

Misconception: If an object is moving at a constant speed, it is not accelerating.

Clarification: This is only true for motion in a straight line. In circular motion, even if the speed is constant, the velocity is changing because the direction is changing. This change in velocity means that the object is accelerating, specifically undergoing centripetal acceleration.

9.3. Centripetal Force Does Work

Misconception: Centripetal force does work on an object in uniform circular motion.

Clarification: Centripetal force does no work on an object in uniform circular motion because the force is always perpendicular to the direction of motion. Work is defined as the force applied in the direction of displacement. Since the centripetal force is perpendicular to the displacement, the work done is zero.

9.4. Heavier Objects Experience Greater Centripetal Acceleration

Misconception: Heavier objects experience greater centripetal acceleration in uniform circular motion.

Clarification: Centripetal acceleration depends on the speed and radius of the circular path, not the mass of the object. While a heavier object requires a greater centripetal force to maintain the same motion, the centripetal acceleration remains the same as long as the speed and radius are constant.

10. Uniforms and Their Relevance in Understanding Physics

While discussing physics, it’s important to note how it intersects with everyday elements, such as uniforms. At onlineuniforms.net, we understand the importance of providing uniforms that meet the needs of various professions and industries. Whether it’s ensuring that medical professionals have comfortable and functional scrubs or that students have durable and appropriate school uniforms, our products reflect an understanding of practical applications.

10.1. Uniform Design and Physics Principles

The design of uniforms often incorporates principles of physics to enhance comfort, safety, and functionality. For example, the choice of materials, such as lightweight and breathable fabrics, can help regulate body temperature and reduce fatigue. The cut and fit of the uniform can also be optimized to allow for ease of movement and flexibility, crucial for many jobs.

10.2. Safety Uniforms

In certain professions, uniforms play a critical role in ensuring safety. High-visibility clothing, for instance, uses reflective materials to make workers more visible in low-light conditions, reducing the risk of accidents. These materials are designed based on principles of light reflection and refraction.

10.3. Uniforms in Sports and Physical Activities

Uniforms designed for sports and physical activities are engineered to optimize performance. Aerodynamic designs can reduce air resistance, while moisture-wicking fabrics help keep athletes dry and comfortable. The design and materials are chosen based on principles of fluid dynamics and thermodynamics.

11. Summary: Key Takeaways on Uniform Circular Motion

Uniform circular motion is characterized by constant speed along a circular path, but with continuously changing velocity direction.
It is not uniformly accelerated motion because the direction of centripetal acceleration constantly changes.
Centripetal acceleration is always directed towards the center of the circle and has a magnitude of ( a_c = frac{v^2}{r} ) or ( a_c = romega^2 ).
Centripetal force is the net force causing an object to move in a circular path, provided by tension, gravity, friction, or normal force.
Non-uniform circular motion involves both centripetal and tangential acceleration.
The Coriolis effect is an apparent deflection of moving objects viewed from a rotating reference frame.

12. Frequently Asked Questions (FAQs) About Uniform Circular Motion

What is uniform circular motion?
- Uniform circular motion is the movement of an object at a constant speed along a circular path.
Is uniform circular motion an example of uniformly accelerated motion?
- No, uniform circular motion is not uniformly accelerated motion because the direction of the acceleration (centripetal acceleration) is constantly changing.
What is centripetal acceleration?
- Centripetal acceleration is the acceleration that causes an object to move in a circular path. It is always directed towards the center of the circle.
How is centripetal acceleration calculated?
- Centripetal acceleration can be calculated using the formula ( a_c = frac{v^2}{r} ) or ( a_c = romega^2 ), where ( v ) is the speed, ( r ) is the radius, and ( omega ) is the angular velocity.
What is centripetal force?
- Centripetal force is the net force that causes an object to move in a circular path. It is always directed towards the center of the circle.
What provides the centripetal force in different scenarios?
- The centripetal force can be provided by tension in a string, gravity, friction, or normal force, depending on the situation.
What is non-uniform circular motion?
- Non-uniform circular motion occurs when an object moves along a circular path with a changing speed. It involves both centripetal and tangential acceleration.
What is tangential acceleration?
- Tangential acceleration is the component of acceleration that is tangent to the circular path, causing the object to change its speed.
What is the Coriolis effect?
- The Coriolis effect is an apparent deflection of moving objects when viewed from a rotating reference frame. It is significant in meteorology and oceanography.
How does moment of inertia relate to circular motion?
- Moment of inertia measures an object’s resistance to rotational motion and relates torque to angular acceleration.

13. Take the Next Step: Explore Uniform Options with Onlineuniforms.net

Understanding the principles of physics, including uniform circular motion, is essential in many fields. At onlineuniforms.net, we apply these principles to design and provide uniforms that meet the diverse needs of professionals, students, and organizations. From comfortable medical scrubs to high-performance athletic wear, our products combine functionality, safety, and style.

Are you looking for high-quality uniforms that meet your specific requirements? Visit onlineuniforms.net today to explore our extensive collection, request a quote, and contact our expert team for personalized assistance. Let us help you find the perfect uniform solutions that enhance your performance and represent your brand with pride. Contact us at:

Address: 1515 Commerce St, Dallas, TX 75201, United States

Phone: +1 (214) 651-8600

Website: onlineuniforms.net

We look forward to assisting you!