Non-uniform circular motion occurs when an object moves along a circular path with a changing speed. This contrasts with uniform circular motion, where the speed remains constant.
What is Non-Uniform Circular Motion?
In uniform circular motion, an object traverses a circular path at a constant speed. However, in non-uniform circular motion, the defining characteristic is the change in speed as the object moves along its circular trajectory. It’s crucial to note that while the direction of the velocity is always changing in circular motion (hence acceleration exists), in non-uniform motion, the magnitude of the velocity vector, representing speed, also varies.
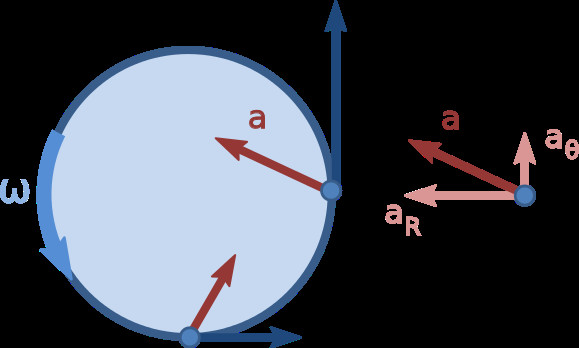Non-Uniform Circular Motion Diagram: Visual representation showing changing velocity vectors and speed in circular motion.
Diagram of Non-Uniform Circular Motion: This diagram illustrates non-uniform circular motion, where you can observe the changing lengths of the velocity vectors, indicating a change in speed over time as the object moves along the circular path.
Radial and Tangential Acceleration in Non-Uniform Motion
The concept of changing speed in circular motion has significant implications for acceleration. We know that for any circular motion, there must be a radial acceleration (also known as centripetal acceleration) directed towards the center of the circle to constantly change the direction of the velocity. This radial acceleration is given by:
(a_r = frac{v^2}{r})
Where:
- (a_r) is the radial acceleration
- (v) is the instantaneous speed of the object
- (r) is the radius of the circular path
In non-uniform circular motion, because the speed (v) is not constant, the magnitude of the radial acceleration (a_r) will also change. We can consider two primary scenarios:
1. Constant Radius with Varying Speed: Imagine a car speeding up and slowing down while driving around a circular track. The radius of the track remains constant. As the car’s speed (v) changes, the radial acceleration required to keep it on the circular path also changes. A higher speed necessitates a larger radial acceleration (and consequently, a greater centripetal force), and vice versa.
2. Constant Radial Force with Varying Speed and Radius: Consider a satellite orbiting a planet. While the gravitational force (providing the centripetal force) might be considered somewhat constant over a short period, changes in the satellite’s speed can lead to changes in the radius of its orbit. If the satellite speeds up, to maintain a constant radial force, the radius might adjust to a new equilibrium. In this case, both speed and radius can vary, but the relationship described by the centripetal acceleration equation must always hold true.
The Role of Tangential Acceleration
It’s crucial to understand that radial or centripetal force and acceleration are responsible for changing the direction of velocity, not its magnitude (speed). To change the speed of an object in circular motion, we need a force acting tangentially to the circular path. This tangential force results in tangential acceleration ((a_t)).
Tangential acceleration is the component of acceleration responsible for the change in the magnitude of the velocity (speed). It acts along the tangent to the circular path at any point and is directly related to the change in angular speed.
Non-Uniform Angular Velocity
Since angular velocity ((omega)) is defined as (omega = frac{v}{r}), and in non-uniform circular motion, the linear speed (v) is changing (and potentially the radius (r) as well in some scenarios), it follows that the angular velocity in non-uniform circular motion is not constant. The object’s rate of rotation around the circular path will either increase or decrease as its speed changes.
Conclusion
Non-uniform circular motion is a more complex but realistic scenario compared to uniform circular motion. It involves changes in speed, leading to variations in radial acceleration and the introduction of tangential acceleration. Understanding both radial and tangential components of acceleration is essential to fully describe and analyze motion along a circular path when the speed is not constant. In such motion, the angular velocity is also not constant, reflecting the changing rate of rotation.
