Uniform Circular Motion is a specific type of motion where an object moves in a circular path at a constant speed. While the speed remains constant, the object’s velocity is continuously changing because its direction of motion is always changing. At any point in time during uniform circular motion, the object’s instantaneous velocity vector is directed tangent to the circular path. This means the object is always moving along the edge of the circle at that moment.
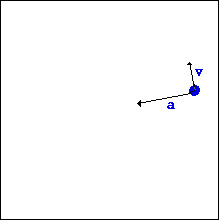Animation depicting uniform circular motion, illustrating tangential velocity and centripetal acceleration vectors.
It’s crucial to understand that an object in uniform circular motion is constantly accelerating, even if its speed is constant. Acceleration is defined as a change in velocity, and velocity is a vector quantity that includes both speed and direction. Since the direction of the object’s motion is always changing as it moves in a circle, its velocity is changing, and therefore it is accelerating. This acceleration in uniform circular motion is always directed towards the center of the circle. We call this acceleration centripetal acceleration or radial acceleration.
Finally, let’s consider the net force acting on an object undergoing uniform circular motion. For an object to move in a circle, there must be a net force acting upon it directed towards the center of the circle. This force is known as the centripetal force. Without a centripetal force, an object would naturally move in a straight line, according to Newton’s first law of motion (the law of inertia). The centripetal force is always perpendicular to the object’s velocity, causing it to change direction continuously and move in a circular path. This inward net force is essential for maintaining uniform circular motion.
For a deeper dive into related physics concepts, explore these resources:
Velocity
Acceleration
Net Force and Acceleration
Circular Motion and Tangential Velocity
Circular Motion and Acceleration
The Centripetal Force Requirement
Return to Animations Index
