Are you looking for clarity on uniform circular motion and its constant quantities? At onlineuniforms.net, we understand the importance of precision, whether it’s in physics or selecting the perfect uniform. Let’s explore what remains constant in uniform circular motion and how that knowledge can be as reliable as our uniform offerings. We provide top-notch uniforms that ensure you always look and feel your best.
1. Understanding Uniform Circular Motion
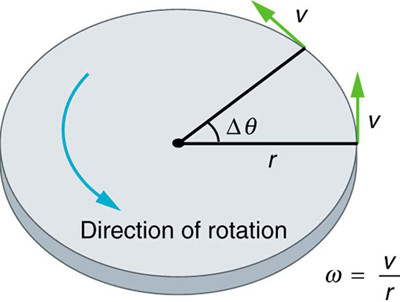
Uniform circular motion (UCM) is defined as the motion of an object traveling at a constant speed along a circular path. But which quantities remain unchanged during this motion?
The quantity that is constant in uniform circular motion is speed. While the velocity (which includes both speed and direction) changes continuously due to the constant change in direction, the speed remains the same.
1.1 Key Aspects of Uniform Circular Motion
- Constant Speed: The object moves at a steady pace around the circle.
- Changing Velocity: The direction of motion is always changing, so the velocity is not constant.
- Centripetal Acceleration: There is acceleration directed towards the center of the circle, necessary to keep the object moving in a circle.
- Constant Radius: The object maintains a fixed distance from the center of the circular path.
1.2 Why Speed Is Constant
In UCM, no force acts in the direction of motion to change the object’s speed. The force acting on the object is centripetal force, which is always directed towards the center of the circle, perpendicular to the object’s velocity. This force only changes the direction of the velocity, not its magnitude.
2. Quantities in Uniform Circular Motion
To fully understand what remains constant, let’s look at the different quantities involved in uniform circular motion.
2.1 Speed vs. Velocity
- Speed: As mentioned, speed remains constant. If an object is moving at 5 m/s, it maintains that speed throughout the motion.
- Velocity: Velocity is a vector quantity, meaning it has both magnitude (speed) and direction. In UCM, the direction is always changing, thus the velocity is not constant.
2.2 Acceleration
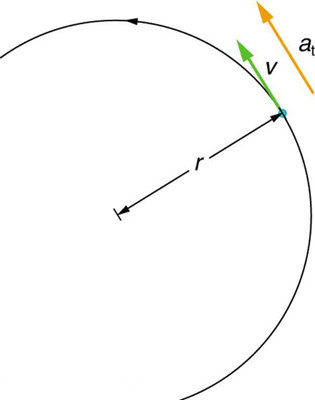
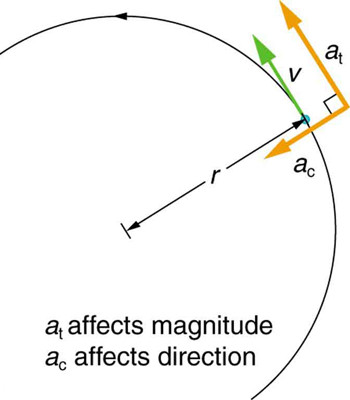
- Centripetal Acceleration: This acceleration is always directed towards the center of the circle and is responsible for changing the direction of the velocity. Its magnitude is constant and given by ( a_c = frac{v^2}{r} ), where ( v ) is the speed and ( r ) is the radius of the circle.
- Tangential Acceleration: In UCM, tangential acceleration is zero. If there were tangential acceleration, it would change the speed of the object, making the motion non-uniform.
2.3 Angular Quantities
- Angular Speed ((omega)): This is the rate at which the object rotates, measured in radians per second (rad/s). In UCM, angular speed is constant.
- Angular Velocity: Similar to linear velocity, angular velocity includes both angular speed and direction. In UCM, angular velocity is constant because both angular speed and the axis of rotation remain fixed.
- Angular Acceleration ((alpha)): Since the angular velocity is constant in UCM, the angular acceleration is zero.
3. Formulas and Relationships
To formalize our understanding, let’s look at some key formulas related to uniform circular motion:
3.1 Speed and Angular Speed
The relationship between linear speed (( v )) and angular speed (( omega )) is given by:
[ v = romega ]
where ( r ) is the radius of the circular path. Since both ( v ) and ( omega ) are constant in UCM, this relationship holds true throughout the motion.
3.2 Centripetal Acceleration
The magnitude of centripetal acceleration (( a_c )) is given by:
[ a_c = frac{v^2}{r} = romega^2 ]
Since ( v ), ( r ), and ( omega ) are constant in UCM, the magnitude of ( a_c ) is also constant, although its direction continuously changes.
3.3 Period and Frequency
- Period (T): The time it takes for one complete revolution around the circle.
- Frequency (f): The number of revolutions per unit time.
They are related by:
[ T = frac{1}{f} ]
And the speed can also be expressed as:
[ v = frac{2pi r}{T} ]
Since ( v ) and ( r ) are constant in UCM, the period ( T ) and frequency ( f ) are also constant.
4. Real-World Examples
Uniform circular motion can be seen in various real-world scenarios, although perfectly uniform motion is an idealization.
4.1 Examples of Uniform Circular Motion
- A satellite orbiting the Earth at a constant altitude and speed: While the orbit is not perfectly circular and the speed may vary slightly, it’s a good approximation of UCM.
- A record spinning on a turntable: The points on the record move in UCM around the center.
- The tip of a fan blade rotating at a constant rate: Each point on the tip follows a circular path at a constant speed.
4.2 Non-Examples of Uniform Circular Motion
- A car speeding up around a circular track: This is non-uniform circular motion because the speed is changing.
- A pendulum swinging: The pendulum’s speed changes as it swings back and forth, and it doesn’t complete a full circle.
5. Non-Uniform Circular Motion
To contrast with UCM, let’s briefly discuss non-uniform circular motion (NUCM).
5.1 Definition
Non-uniform circular motion occurs when an object moves along a circular path with a changing speed.
5.2 Key Differences from UCM
- Changing Speed: The object’s speed is not constant.
- Tangential Acceleration: There is tangential acceleration that causes the change in speed.
- Variable Angular Speed: The angular speed (( omega )) is also changing.
5.3 Examples of Non-Uniform Circular Motion
- A roller coaster going through a loop: The speed changes as it goes up and down the loop.
- A merry-go-round starting up or slowing down: During the start and stop phases, the angular speed is not constant.
6. Practical Applications of Understanding Circular Motion
Understanding circular motion isn’t just theoretical; it has practical applications in various fields.
6.1 Engineering
- Designing rotating machinery: Engineers need to understand the forces and accelerations involved in circular motion to design safe and efficient rotating parts.
- Calculating the stability of vehicles: Understanding circular motion helps in designing stable vehicles that can navigate turns safely.
6.2 Physics
- Studying celestial mechanics: Understanding UCM and NUCM is crucial for studying the motion of planets, stars, and galaxies.
- Developing new technologies: Principles of circular motion are used in developing technologies like centrifuges and particle accelerators.
7. How to Calculate Quantities in Uniform Circular Motion
Let’s go through some examples of how to calculate quantities in uniform circular motion.
7.1 Example 1: Calculating Speed
Problem: A car is moving around a circular track with a radius of 50 meters. It completes one lap in 20 seconds. Calculate its speed.
Solution:
- Identify the given values:
- Radius (( r )) = 50 m
- Time for one lap (( T )) = 20 s
- Use the formula for speed:
[ v = frac{2pi r}{T} ] - Plug in the values:
[ v = frac{2pi (50)}{20} ] - Calculate:
[ v = frac{314.16}{20} ]
[ v approx 15.71 , text{m/s} ]
So, the car’s speed is approximately 15.71 meters per second.
7.2 Example 2: Calculating Centripetal Acceleration
Problem: A ball is attached to a string and swung in a horizontal circle with a radius of 1.5 meters. If the ball’s speed is 3 m/s, what is its centripetal acceleration?
Solution:
- Identify the given values:
- Radius (( r )) = 1.5 m
- Speed (( v )) = 3 m/s
- Use the formula for centripetal acceleration:
[ a_c = frac{v^2}{r} ] - Plug in the values:
[ a_c = frac{(3)^2}{1.5} ] - Calculate:
[ a_c = frac{9}{1.5} ]
[ a_c = 6 , text{m/s}^2 ]
So, the ball’s centripetal acceleration is 6 meters per second squared.
8. Onlineuniforms.net: Consistent Quality and Service
Just as speed is constant in uniform circular motion, at onlineuniforms.net, we strive to maintain constant quality in our products and services. Whether you’re outfitting a team, school, or business, you can rely on us for consistent excellence.
8.1 Why Choose Onlineuniforms.net?
- Wide Variety of Uniforms: We offer a diverse selection of uniforms for various industries and needs.
- Customization Options: Tailor your uniforms with logos, names, and specific designs.
- High-Quality Materials: Our uniforms are made from durable, comfortable materials.
- Excellent Customer Service: We are committed to providing exceptional support and assistance.
- Reliable Delivery: Count on us for timely and accurate delivery of your orders.
8.2 Meeting Your Uniform Needs
We understand the challenges customers face when searching for the right uniforms:
- Finding a reliable online uniform supplier: We are a trusted source with a proven track record.
- Selecting the right uniform for the job: Our experts can help you choose the best options for your specific needs.
- Ensuring the right fit for everyone: We provide detailed sizing guides and customization options to guarantee a perfect fit.
- Customizing uniforms with logos and branding: We offer professional customization services to showcase your brand.
- Ordering uniforms in bulk and receiving them on time: Our efficient ordering and delivery process ensures you get your uniforms when you need them.
At onlineuniforms.net, we provide solutions to these challenges by offering:
- A comprehensive range of uniforms for various professions, including medical, educational, and corporate sectors.
- Detailed size charts and fitting guides to help you select the correct sizes.
- Customization services such as embroidery and printing to add your logo or design.
- Expert advice on fabric types and uniform styles to suit your specific requirements.
- Bulk ordering options with fast and reliable delivery across the USA.
9. Testimonials and Reviews
Don’t just take our word for it. Here’s what our customers have to say:
- “Onlineuniforms.net has been our go-to supplier for years. The quality is consistently excellent, and their customization options are fantastic.” – John S., Business Owner
- “We needed a large order of school uniforms quickly, and onlineuniforms.net delivered! The uniforms were high-quality and arrived on time.” – Mary L., School Principal
- “The customer service team at onlineuniforms.net is outstanding. They helped us find the perfect uniforms for our medical staff.” – Dr. Emily R., Hospital Administrator
10. Optimizing Uniform Choices for Different Professions
Choosing the right uniform involves considering the specific needs and demands of various professions.
10.1 Medical Uniforms
- Requirements: Comfort, durability, hygiene, and functionality.
- Recommended Fabrics: Cotton-polyester blends for breathability and stain resistance.
- Key Features: Multiple pockets, easy-to-clean materials, and professional appearance.
10.2 Educational Uniforms
- Requirements: Comfort, durability, safety, and compliance with school policies.
- Recommended Fabrics: Durable and easy-to-maintain fabrics like twill or poplin.
- Key Features: Reinforced stitching, adjustable fits, and options for customization with school logos.
10.3 Corporate Uniforms
- Requirements: Professional appearance, comfort, durability, and brand representation.
- Recommended Fabrics: Wrinkle-resistant materials such as microfiber or performance blends.
- Key Features: Tailored fits, options for embroidery, and coordinated styles for different roles.
10.4 Hospitality Uniforms
- Requirements: Comfort, style, durability, and easy maintenance.
- Recommended Fabrics: Stain-resistant and breathable fabrics like polyester blends or linen.
- Key Features: Stylish designs, functional pockets, and options for personalization with company logos.
11. Tips for Maintaining Uniform Quality
To ensure your uniforms last longer and maintain their appearance, follow these maintenance tips:
11.1 Washing
- Read the Label: Always follow the manufacturer’s instructions on the garment label.
- Turn Inside Out: Protect the outer fabric by washing uniforms inside out.
- Use Cold Water: Prevent fading and shrinkage by washing in cold water.
- Mild Detergent: Use a mild detergent to avoid damaging the fabric.
- Avoid Overloading: Ensure thorough cleaning by not overloading the washing machine.
11.2 Drying
- Low Heat: Dry uniforms on a low heat setting or hang them to air dry.
- Avoid Over-Drying: Prevent shrinkage and fabric damage by avoiding over-drying.
- Remove Promptly: Take uniforms out of the dryer as soon as they are dry to minimize wrinkles.
11.3 Ironing
- Use Appropriate Settings: Use the iron setting recommended for the fabric type.
- Iron Inside Out: Protect the outer fabric by ironing uniforms inside out.
- Use a Pressing Cloth: Prevent shine and damage by using a pressing cloth.
11.4 Storage
- Hang Uniforms: Use sturdy hangers to maintain the shape of the uniforms.
- Store in a Cool, Dry Place: Prevent mildew and fabric damage by storing uniforms in a cool, dry place.
By following these tips, you can extend the life of your uniforms and ensure they always look their best.
12. Uniform Trends and Innovations
Staying updated with the latest trends and innovations in uniform design ensures that your team looks modern and professional.
12.1 Sustainable Fabrics
- Eco-Friendly Options: Choose uniforms made from sustainable materials like organic cotton, recycled polyester, or bamboo.
- Benefits: Reduces environmental impact and promotes a positive brand image.
12.2 Performance Fabrics
- Moisture-Wicking: Keeps the wearer comfortable by drawing sweat away from the body.
- Antimicrobial: Prevents the growth of bacteria and odors.
- UV Protection: Protects against harmful UV rays during outdoor activities.
12.3 Smart Uniforms
- Wearable Technology: Incorporate sensors for monitoring health and safety in high-risk environments.
- Enhanced Communication: Integrate communication devices for improved coordination and response times.
12.4 Custom Design Elements
- Unique Branding: Incorporate custom logos, colors, and patterns to create a distinctive brand identity.
- Functional Design: Add practical features such as specialized pockets or adjustable closures for enhanced usability.
13. Frequently Asked Questions (FAQ) About Uniform Circular Motion
Here are some frequently asked questions to further clarify the concept of uniform circular motion.
13.1 What is uniform circular motion?
Uniform circular motion is the motion of an object moving at a constant speed along a circular path.
13.2 What quantities are constant in uniform circular motion?
The speed and radius are constant. The magnitude of centripetal acceleration is also constant, though its direction changes.
13.3 Why is velocity not constant in uniform circular motion?
Although the speed is constant, the direction of the object’s motion is always changing, making the velocity (which includes both speed and direction) non-constant.
13.4 What is centripetal acceleration?
Centripetal acceleration is the acceleration that keeps an object moving in a circle. It is always directed towards the center of the circle.
13.5 Is there tangential acceleration in uniform circular motion?
No, tangential acceleration is zero in uniform circular motion because the speed is constant.
13.6 What is non-uniform circular motion?
Non-uniform circular motion is when an object moves along a circular path with a changing speed.
13.7 How is angular speed related to linear speed in uniform circular motion?
The relationship is ( v = romega ), where ( v ) is the linear speed, ( r ) is the radius, and ( omega ) is the angular speed.
13.8 What are some real-world examples of uniform circular motion?
Examples include a satellite orbiting Earth at a constant altitude and speed, and a record spinning on a turntable.
13.9 How do you calculate speed in uniform circular motion?
Speed can be calculated using the formula ( v = frac{2pi r}{T} ), where ( r ) is the radius and ( T ) is the period.
13.10 How do you calculate centripetal acceleration?
Centripetal acceleration can be calculated using the formula ( a_c = frac{v^2}{r} ), where ( v ) is the speed and ( r ) is the radius.
14. Conclusion
Understanding uniform circular motion involves knowing which quantities remain constant and why. Just as speed remains constant in UCM, onlineuniforms.net remains consistent in providing high-quality uniforms and exceptional service.
Ready to outfit your team or organization with reliable, high-quality uniforms? Contact us today!
Address: 1515 Commerce St, Dallas, TX 75201, United States
Phone: +1 (214) 651-8600
Website: onlineuniforms.net
Visit onlineuniforms.net to explore our wide range of uniform options, request a quote, and discover how we can meet your specific uniform needs. Trust us to deliver consistent quality and service, every time.
Medical professionals in blue scrubs, showcasing the comfort and professionalism onlineuniforms.net offers in medical attire.
Students in school uniforms, highlighting the durability and style available at onlineuniforms.net for educational institutions.
Corporate employees in branded uniforms, demonstrating the customization options provided by onlineuniforms.net for businesses.
