How Does A Solid Sphere With A Uniformly Distributed Mass Behave?

A solid sphere with a uniformly distributed mass creates a gravitational field that attracts other objects, and onlineuniforms.net offers durable uniforms suitable for various fields of work related to physics and engineering. Understanding the physics behind uniform mass distribution will give you a lot more to work with. These are essential for keeping our professionals safe and presentable, reflecting our commitment to quality.

1. What is the Law of Universal Gravitation?

The Law of Universal Gravitation states that every point mass attracts every other point mass in the universe with a force pointing in a straight line between the centers of mass of both points. This force is proportional to the product of the masses and inversely proportional to the square of the distance between them. In simpler terms, the more massive the objects and the closer they are, the stronger the gravitational pull.

1.1. Expressing the Law Mathematically

The Law of Universal Gravitation can be expressed mathematically as:

F = G(Mm/r^2)

Where:

• F represents the gravitational force in Newtons.
• M and m are the two masses in kilograms.
• r is the distance between the centers of the masses in meters.
• G is the gravitational constant, approximately 6.674 x 10^-11 N(m/kg)^2.

1.2. Historical Context of the Law

Sir Isaac Newton formulated the Law of Universal Gravitation after observing an apple falling from a tree. He realized that the same force pulling the apple to the ground also governs the motion of the moon around the Earth. This groundbreaking discovery revolutionized our understanding of the universe.

1.3. Significance of the Gravitational Constant (G)

The gravitational constant (G) is a fundamental constant of nature that determines the strength of the gravitational force. Its value was not accurately determined until Henry Cavendish’s experiment, which allowed scientists to quantify the gravitational force between objects.

2. How Does the Shell Theorem Relate to Spherical Bodies?

The Shell Theorem provides a simplified way to calculate the gravitational force exerted by spherically symmetric objects. It states that a spherically symmetric object affects other objects gravitationally as if all its mass were concentrated at its center. This theorem simplifies calculations and helps understand the gravitational behavior of objects like planets and stars.

2.1. Formulating the Shell Theorem

The Shell Theorem has two main components:

1. A spherically symmetric object affects other objects gravitationally as if all its mass were concentrated at its center.
2. If the object is a spherically symmetric shell (a hollow ball), the net gravitational force on a body inside it is zero.

2.2. Implications for Spherically Symmetric Bodies

The Shell Theorem simplifies the calculation of gravitational forces for spherically symmetric objects. Instead of integrating over the entire volume of the object, one can treat it as a point mass located at its center. This is particularly useful for astronomical calculations.

2.3. Applying the Shell Theorem

Consider a planet with a uniform density. According to the Shell Theorem, the gravitational force exerted by the planet on an object outside it can be calculated by treating the planet as a point mass at its center. For an object inside a hollow spherical shell, the net gravitational force is zero, meaning the object experiences weightlessness.

3. What is the Gravitational Attraction of Spherical Bodies?

The gravitational attraction of spherical bodies depends on the distribution of mass within the sphere. For a uniformly distributed mass, the gravitational force can be calculated using the Shell Theorem. However, for non-uniform distributions, more complex calculations are required.

3.1. Universal Gravitation for Spherically Symmetric Bodies

For spherically symmetric bodies, the gravitational force between two points of mass is proportional to the magnitudes of their masses and inversely proportional to the square of their separation.

F = G(mM/d^2)

Where:

• F is the gravitational force.
• G is the gravitational constant.
• m and M are the masses of the two bodies.
• d is the distance between their centers.

3.2. Understanding the Shell Theorem

Isaac Newton proved the Shell Theorem, which states that a spherically symmetric object affects other objects gravitationally as if all of its mass were concentrated at its center. Additionally, if the object is a spherically symmetric shell, the net gravitational force on a body inside of it is zero.

3.3. How to Apply These Principles

When finding the force of gravity exerted on a ball of 10 kg, the distance measured from the ball is taken from the ball’s center of mass to the earth’s center of mass. Understanding these principles helps in calculating gravitational forces in various scenarios.

4. What Happens Inside a Hollow Spherical Shell?

Inside a hollow spherical shell, the net gravitational force on any object is zero. This is because the gravitational forces from all parts of the shell cancel each other out. This phenomenon has significant implications for understanding gravitational shielding and the behavior of objects in enclosed spaces.

4.1. Case 1: A Hollow Spherical Shell

The gravitational force acting by a spherically symmetric shell upon a point mass inside it is the vector sum of gravitational forces acted by each part of the shell. This vector sum is equal to zero. Therefore, a mass m within a spherically symmetric shell of mass M will feel no net force.

4.2. Net Gravitational Force Outside the Shell

The net gravitational force that a spherical shell of mass M exerts on a body outside of it is the vector sum of the gravitational forces acted by each part of the shell on the outside object. This adds up to a net force acting as if mass M is concentrated on a point at the center of the sphere.

4.3. Visualizing the Shell Theorem

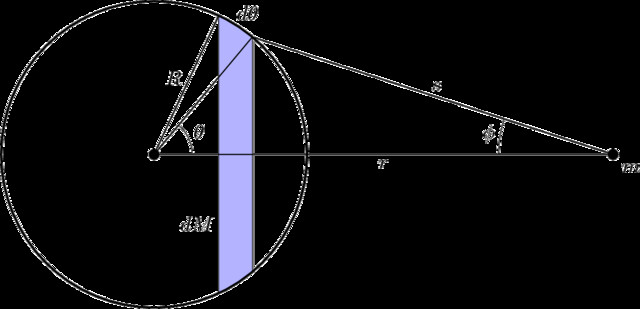Diagram used in the proof of the Shell Theorem

This diagram outlines the geometry considered when proving The Shell Theorem. In this case, a spherical shell of mass M (left side of figure) exerts a force on mass m (right side of the figure) outside of it. The surface area of a thin slice of the sphere is shown in color.

5. What is the Force Exerted by a Solid, Uniform Sphere?

A solid, uniform sphere exerts a gravitational force that depends on the distance from its center. Inside the sphere, the force increases linearly with distance, while outside the sphere, the force decreases with the square of the distance. This behavior is crucial for understanding the gravitational environment within and around planets.

5.1. Case 2: A Solid, Uniform Sphere

Consider a solid, uniform sphere of mass M and radius R, exerting a force on a body of mass m at a radius d inside of it (d<R). The force is given by:

F = (GmMinner) / d^2

Where:

• Minner is the mass enclosed within the radius d.
• Minner = (4/3)πd^3ρ
• ρ is the mass density of the sphere (assuming uniform distribution).

5.2. Combining Equations

Combining the above equations, we get:

F = (4/3)πGmρd

This shows that mass m feels a force that is linearly proportional to its distance, d, from the sphere’s center of mass.

5.3. Gravitational Force Outside the Sphere

As in the case of hollow spherical shells, the net gravitational force that a solid sphere of uniformly distributed mass M exerts on a body outside of it is the vector sum of the gravitational forces acted by each shell of the sphere on the outside object. The resulting net gravitational force acts as if mass M is concentrated on a point at the center of the sphere, which is the center of mass (COM).

6. How Do We Calculate Gravitational Force for Extended Bodies?

For bodies with spatial extent, gravitational force is calculated by summing the contributions of point masses that constitute them. This involves integrating the force over the extents of the two bodies, which can be simplified using the Shell Theorem for spherically symmetric objects.

6.1. Calculating Gravitational Force

Newton’s law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

F = G(m1m2/r^2)

Where:

• F is the force between the masses.
• G is the gravitational constant.
• m1 is the first mass.
• m2 is the second mass.
• r is the distance between the centers of the masses.

6.2. Applying Integration

If the bodies in question have spatial extent, the gravitational force between them is calculated by summing the contributions of the notional point masses which constitute the bodies. In the limit, as the component point masses become infinitely small, this entails integrating the force (in vector form) over the extents of the two bodies.

6.3. Simplifying with Spherical Symmetry

An object with a spherically-symmetric distribution of mass exerts the same gravitational attraction on external bodies as if all the object’s mass were concentrated at a point at its center. This simplification is crucial for calculations involving planets and stars.

7. How Does the Shell Theorem Apply Inside a Sphere?

For points inside a spherically-symmetric distribution of matter, Newton’s Shell theorem can be used to find the gravitational force. The theorem provides insights into how different parts of the mass distribution affect the gravitational force measured at a point located a distance from the center of the mass distribution.

7.1. Understanding the Theorem

The Shell Theorem tells us how different parts of the mass distribution affect the gravitational force measured at a point located a distance r0 from the center of the mass distribution:

1. The portion of the mass that is located at radii r<r0 contributes to the net gravitational force at the distance r0.
2. The portion of the mass that is located at radii r>r0 exerts no net gravitational force at the distance r0 from the center.

7.2. Consequences of the Theorem

Within a shell of uniform thickness and density, there is no net gravitational acceleration anywhere within the hollow sphere. Inside a uniform sphere, the gravity increases linearly with the distance from the center.

7.3. Earth’s Gravity

The gravity of the Earth may be highest at the core/mantle boundary. This is due to the distribution of mass within the Earth, where the core is denser than the mantle.

8. How is the Weight of the Earth Calculated?

Calculating the weight of the Earth involves using Newton’s Law of Universal Gravitation and the experimentally verified value of acceleration due to gravity. By equating Newton’s second law with his law of universal gravitation, we can determine the mass of the Earth.

8.1. Using Newton’s Law

The weight of the Earth is calculated using the formula:

F = G(Mm/r^2)

Where:

• F is the gravitational force.
• G is the gravitational constant.
• M is the mass of the Earth.
• m is the mass of an object on Earth.
• r is the radius of the Earth.

8.2. Experimental Verification

By equating Newton’s second law (F = ma) with his law of universal gravitation and inputting the experimentally verified value of 9.8 m/s^2 for acceleration (a), the mass of Earth is calculated to be approximately 5.96 x 10^24 kg.

8.3. Implications for Gravitational Fields

This calculation makes the Earth’s weight calculable given any gravitational field. It also helps in understanding the gravitational forces exerted by other celestial bodies.

9. What are Real-World Applications of These Principles?

These gravitational principles are used in various real-world applications, including satellite navigation, space exploration, and geophysical studies. Understanding these principles is essential for engineers, physicists, and other professionals working in related fields, and onlineuniforms.net offers durable and appropriate attire for these professionals.

9.1. Satellite Navigation

Satellite navigation systems rely on accurate calculations of gravitational forces to determine the position of satellites and provide precise location data.

9.2. Space Exploration

Space missions require a deep understanding of gravitational forces to plan trajectories, calculate fuel consumption, and ensure the safety of spacecraft.

9.3. Geophysical Studies

Geophysical studies use gravitational measurements to map the Earth’s interior, study geological formations, and monitor changes in the Earth’s gravity field.

10. How Can Professionals Benefit from Understanding Gravitational Principles?

Professionals in various fields, such as engineering, physics, and geophysics, can benefit significantly from understanding gravitational principles. This knowledge enhances their ability to design structures, analyze data, and solve complex problems, and onlineuniforms.net provides the necessary professional attire.

10.1. Engineering Applications

Engineers use gravitational principles to design bridges, buildings, and other structures that can withstand gravitational forces and environmental loads.

10.2. Physics Research

Physicists rely on gravitational theories to study the universe, understand the behavior of celestial bodies, and develop new technologies.

10.3. Geophysical Analysis

Geophysicists use gravitational data to study the Earth’s structure, monitor natural disasters, and explore resources.

FAQ: Solid Sphere with Uniformly Distributed Mass

1. What is a solid sphere with uniformly distributed mass?

A solid sphere with uniformly distributed mass is a sphere where the mass is evenly spread throughout its volume, meaning the density is constant at every point within the sphere.

2. How does gravity behave inside a solid sphere with uniformly distributed mass?

Inside such a sphere, the gravitational force increases linearly with distance from the center. At the center, gravity is zero, and it increases until you reach the surface.

3. What is the Shell Theorem and how does it apply to solid spheres?

The Shell Theorem states that for a spherically symmetric object, the gravitational force outside the object is the same as if all its mass were concentrated at its center. Inside a hollow sphere, the gravitational force is zero. For a solid sphere, it helps calculate the force at different points.

4. How do you calculate the gravitational force exerted by a solid sphere on an object outside it?

You can calculate it using Newton’s Law of Universal Gravitation, treating the sphere as a point mass located at its center. The formula is F = G(Mm/r^2), where F is the force, G is the gravitational constant, M is the mass of the sphere, m is the mass of the object, and r is the distance from the center of the sphere to the object.

5. Does the density of the sphere affect the gravitational force?

Yes, the density of the sphere directly affects the gravitational force. A higher density means more mass packed into the same volume, resulting in a stronger gravitational pull.

6. What happens if the mass distribution within the sphere is not uniform?

If the mass distribution is not uniform, the gravitational force is more complex to calculate. You would need to integrate over the mass distribution to find the net gravitational force.

7. Can the principles of a solid sphere with uniformly distributed mass be applied to planets?

While planets are not perfectly uniform, the principles can be a useful approximation. For more accurate calculations, you need to consider the actual mass distribution within the planet.

8. How is the gravitational constant (G) used in these calculations?

The gravitational constant (G) is a fundamental constant that relates the gravitational force to the masses and distance involved. It is essential for accurately calculating gravitational forces.

9. What are some real-world applications of understanding the gravity of solid spheres?

Real-world applications include calculating satellite orbits, understanding planetary motion, and designing structures that can withstand gravitational forces.

10. Where can I find reliable uniforms for professionals working with these principles?

You can find reliable uniforms at onlineuniforms.net, which offers a variety of durable and appropriate attire for professionals in fields like engineering, physics, and geophysics.

Understanding the behavior of a solid sphere with a uniformly distributed mass is crucial for various scientific and engineering applications. Whether you are calculating satellite orbits or designing structures, these principles provide a foundation for accurate and reliable results. At onlineuniforms.net, we support professionals in these fields by providing high-quality, durable uniforms that meet the demands of their work.

Ready to explore our range of uniforms? Visit onlineuniforms.net today to find the perfect fit for your professional needs. Contact us at +1 (214) 651-8600 or visit our location at 1515 Commerce St, Dallas, TX 75201, United States, for personalized assistance and expert advice.