Do you need to know How To Tell If A Histogram Is Normal Or Uniform for your business needs? Understanding histogram distributions is crucial for businesses aiming to analyze data effectively and make informed decisions, and at onlineuniforms.net, we help you to present data clearly. Knowing whether a histogram is normal or uniform can significantly impact your data interpretation and strategic planning.
1. What Is a Histogram and Why Is It Important?
A histogram is a graphical representation of data that groups data points into specified ranges, showing the frequency of data within each range with bars.
1.1 Visualizing Data Distributions
Histograms are essential for visualizing the distribution of data, which is crucial in many fields. Understanding this distribution helps in identifying patterns, outliers, and underlying trends within the data. For instance, in quality control, a histogram can quickly show if a manufacturing process is producing items within acceptable specifications.
1.2 Key Components of a Histogram
Histograms consist of several key components:
- Bins: These are the ranges into which the data is divided. The width of the bins can affect the appearance and interpretation of the histogram.
- Frequency: This represents the number of data points that fall into each bin. The height of each bar in the histogram corresponds to the frequency of its bin.
- Axes: The x-axis represents the bins (data ranges), and the y-axis represents the frequency.
1.3 Applications Across Industries
Histograms are used across various industries for different purposes:
- Manufacturing: To monitor the consistency of product dimensions.
- Finance: To analyze the distribution of stock prices or investment returns.
- Healthcare: To examine the distribution of patient ages or blood pressure readings.
- Retail: To understand the distribution of customer spending.
1.4 Benefits of Using Histograms
Using histograms offers numerous benefits:
- Data Summarization: Histograms summarize large datasets into a visual format, making it easier to understand the data at a glance.
- Pattern Identification: They help in identifying patterns such as central tendency, spread, and skewness in the data.
- Decision Making: By providing a clear view of the data distribution, histograms aid in making informed decisions.
- Process Monitoring: They can be used to monitor processes and detect any deviations from the norm.
2. Understanding Normal Distribution
A normal distribution, also known as a Gaussian distribution, is a common probability distribution that is symmetrical around the mean, showing that data near the mean are more frequent than data far from the mean.
2.1 Characteristics of a Normal Distribution
The normal distribution has several defining characteristics:
- Symmetry: The distribution is symmetrical around the mean, meaning if you were to draw a line down the center (at the mean), the two halves would be mirror images of each other.
- Bell-Shaped Curve: The histogram of a normal distribution resembles a bell, with the highest point at the mean and the curve tapering off symmetrically on both sides.
- Mean, Median, and Mode: In a perfect normal distribution, the mean, median, and mode are all equal and located at the center of the distribution.
- Standard Deviation: The spread of the data is determined by the standard deviation. A smaller standard deviation indicates that the data is clustered tightly around the mean, while a larger standard deviation indicates a wider spread.
2.2 Visual Cues in a Normal Histogram
When examining a histogram for normality, look for these visual cues:
- Central Peak: The histogram should have a clear peak in the middle, representing the mean of the data.
- Symmetrical Tails: The tails of the histogram should taper off symmetrically on both sides of the peak.
- Smooth Curve: The overall shape of the histogram should approximate a smooth, bell-shaped curve.
2.3 Real-World Examples of Normal Distribution
Normal distributions occur frequently in nature and various real-world scenarios:
- Heights of Adults: The heights of adults in a population often follow a normal distribution, with most people being close to the average height and fewer people being very tall or very short.
- Exam Scores: Standardized test scores, such as those from the SAT or GRE, are often designed to follow a normal distribution.
- Blood Pressure: Blood pressure readings in a healthy population tend to be normally distributed around an average value.
2.4 Importance of Recognizing Normal Distribution
Recognizing a normal distribution is important for several reasons:
- Statistical Inference: Many statistical tests and procedures assume that the data is normally distributed. If the data deviates significantly from normality, these tests may not be valid.
- Prediction: Normal distributions allow for predictions about future data points. For example, you can estimate the probability of observing a value within a certain range.
- Quality Control: In manufacturing, a normal distribution can indicate that a process is stable and under control. Deviations from normality may signal a problem that needs to be addressed.
2.5 Common Deviations from Normality
While normal distributions are common, data can also deviate from normality in several ways:
- Skewness: The distribution is asymmetrical, with one tail longer than the other. A right-skewed distribution has a longer tail on the right, while a left-skewed distribution has a longer tail on the left.
- Kurtosis: This refers to the “tailedness” of the distribution. High kurtosis indicates a distribution with heavy tails and a sharp peak, while low kurtosis indicates a distribution with light tails and a flatter peak.
- Multimodal: The distribution has more than one peak, indicating that the data may come from multiple underlying populations.
3. Exploring Uniform Distribution
A uniform distribution, also known as a rectangular distribution, is a probability distribution where all values within a specified range are equally likely.
3.1 Defining Characteristics of a Uniform Distribution
The key characteristics of a uniform distribution include:
- Equal Probability: Every value within the defined range has an equal chance of occurring.
- Rectangular Shape: The histogram of a uniform distribution appears as a rectangle, with a flat top indicating constant frequency across the range.
- Defined Range: The distribution is bounded by a minimum and maximum value, outside of which the probability is zero.
3.2 Visual Cues in a Uniform Histogram
When assessing a histogram for uniform distribution, look for these visual cues:
- Flat Top: The histogram should have a relatively flat top, indicating that all bins have roughly the same frequency.
- No Clear Peak: Unlike a normal distribution, a uniform distribution does not have a distinct peak.
- Consistent Frequency: The frequency of data points should be consistent across the range, with no significant variations.
3.3 Real-World Examples of Uniform Distribution
Uniform distributions can be found in various scenarios:
- Random Number Generators: Ideally, random number generators should produce numbers that are uniformly distributed across a specified range.
- Lottery Numbers: In a fair lottery, each number has an equal chance of being drawn, resulting in a uniform distribution of winning numbers over time.
- Waiting Times: If customers arrive at a store randomly and the service time is constant, the waiting times might approximate a uniform distribution.
3.4 Importance of Recognizing Uniform Distribution
Identifying a uniform distribution is important for several reasons:
- Process Evaluation: It can indicate whether a process is truly random or if there are underlying biases.
- Simulation: Uniform distributions are often used in simulations to model situations where all outcomes are equally likely.
- Resource Allocation: Understanding uniform distributions can help in allocating resources more efficiently, especially when dealing with random events.
3.5 Common Deviations from Uniformity
Data can deviate from uniformity in various ways:
- Gaps: There may be gaps in the distribution where certain values are never observed.
- Clustering: Data points may cluster around certain values, leading to uneven frequencies.
- Trends: There may be increasing or decreasing trends in the frequency of data points across the range.
3.6 Applications of Uniform Distribution in Online Uniforms
At onlineuniforms.net, understanding uniform distribution helps us in several key areas:
- Inventory Management: By analyzing the distribution of uniform sizes ordered by customers, we can ensure that we maintain an adequate stock level for all sizes, avoiding stockouts and meeting customer demand effectively.
- Production Planning: Knowing that each uniform size is equally likely to be ordered allows us to plan our production runs efficiently, ensuring a balanced output across all sizes.
- Quality Control: Monitoring the consistency of uniform dimensions and material quality ensures that each uniform meets our standards, maintaining customer satisfaction.
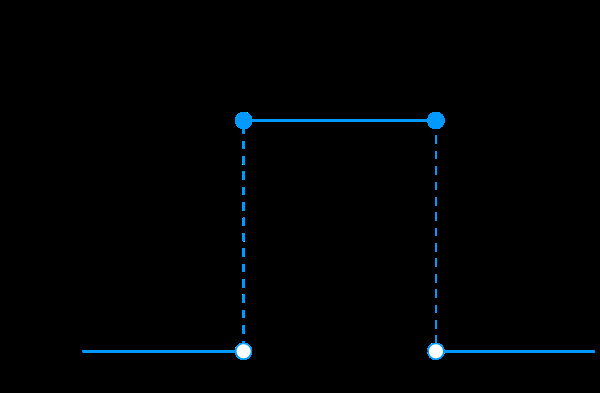 Uniform Distribution Graph Alt Text: A rectangular graph illustrating a uniform distribution, where all values within the range have an equal probability. Keywords: uniform distribution, rectangular graph, statistics, equal probability.
Uniform Distribution Graph Alt Text: A rectangular graph illustrating a uniform distribution, where all values within the range have an equal probability. Keywords: uniform distribution, rectangular graph, statistics, equal probability.
4. Key Differences Between Normal and Uniform Histograms
Differentiating between normal and uniform histograms is essential for accurate data interpretation. Here’s a detailed comparison:
4.1 Shape
- Normal Histogram: Features a bell-shaped curve with a central peak and symmetrical tails.
- Uniform Histogram: Presents a rectangular shape with a flat top, indicating equal frequency across the range.
4.2 Central Tendency
- Normal Histogram: Exhibits a clear central tendency, with the mean, median, and mode located at the center of the distribution.
- Uniform Histogram: Lacks a distinct central tendency, as all values within the range are equally likely.
4.3 Variability
- Normal Histogram: Shows variability around the mean, with data points clustering closer to the center and tapering off towards the tails.
- Uniform Histogram: Displays consistent variability across the range, with no significant variations in frequency.
4.4 Skewness
- Normal Histogram: Ideally, a normal distribution is symmetrical and has zero skewness.
- Uniform Histogram: Uniform distributions also have zero skewness due to their symmetry.
4.5 Kurtosis
- Normal Histogram: Has a kurtosis value close to 3, indicating a moderate peak and tail thickness.
- Uniform Histogram: Has a kurtosis value less than 3, indicating a flatter peak and thinner tails compared to a normal distribution.
4.6 Visual Summary Table
| Feature | Normal Histogram | Uniform Histogram |
|---|---|---|
| Shape | Bell-shaped curve | Rectangular shape |
| Central Tendency | Clear central peak (mean, median, mode) | No distinct central peak |
| Variability | Varies around the mean | Consistent across the range |
| Skewness | Symmetrical (zero skewness) | Symmetrical (zero skewness) |
| Kurtosis | Kurtosis value close to 3 | Kurtosis value less than 3 |
| Real-World Example | Heights of adults, exam scores | Random number generators, lottery numbers |
4.7 Practical Examples in Online Uniforms
- Normal Distribution: If we analyze the distribution of employee sizes for a particular uniform type, we might find a normal distribution, with most employees needing sizes close to the average and fewer needing very small or very large sizes.
- Uniform Distribution: When offering a promotion where every customer has an equal chance of winning a discount, the distribution of discount amounts (e.g., 10%, 20%, 30%) should ideally be uniform, ensuring fairness.
Understanding these differences allows businesses to accurately interpret data and make informed decisions based on the underlying distribution.
5. Statistical Tests to Determine Distribution Type
To rigorously determine whether a dataset follows a normal or uniform distribution, statistical tests are essential. Here are some key tests:
5.1 Tests for Normality
These tests assess how well a dataset fits a normal distribution:
- Shapiro-Wilk Test: This test is particularly effective for small to medium-sized datasets (n < 50). It calculates a W statistic, where values close to 1 indicate that the data is normally distributed.
- Kolmogorov-Smirnov Test: This test compares the cumulative distribution function of the sample data to a standard normal distribution. It is more suitable for larger datasets.
- Anderson-Darling Test: This test is similar to the Kolmogorov-Smirnov test but gives more weight to the tails of the distribution, making it more sensitive to deviations from normality in the tails.
5.2 Tests for Uniformity
These tests evaluate whether a dataset follows a uniform distribution:
- Chi-Square Test: This test compares the observed frequencies of data points in each bin to the expected frequencies under a uniform distribution. A significant p-value indicates that the data does not follow a uniform distribution.
- Kolmogorov-Smirnov Test: As with normality testing, the Kolmogorov-Smirnov test can also be used to test for uniformity by comparing the sample’s cumulative distribution function to that of a uniform distribution.
5.3 How to Interpret Test Results
Interpreting the results of these tests involves examining the p-values:
- P-Value: The p-value represents the probability of observing the test statistic (or a more extreme value) if the null hypothesis is true.
- Significance Level (Alpha): Typically, a significance level of 0.05 is used. If the p-value is less than 0.05, the null hypothesis is rejected, indicating that the data does not follow the specified distribution.
- Null Hypothesis: For normality tests, the null hypothesis is that the data is normally distributed. For uniformity tests, the null hypothesis is that the data is uniformly distributed.
5.4 Practical Application in Online Uniforms
Consider the scenario where onlineuniforms.net wants to analyze the distribution of customer order dates to optimize staffing levels.
-
Scenario: Customer orders are recorded daily, and we want to determine if the orders are uniformly distributed throughout the week or if there are specific days with higher order volumes.
-
Steps:
-
Collect Data: Gather data on the number of orders placed each day of the week over a representative period.
-
Formulate Hypotheses:
- Null Hypothesis (H0): The number of orders is uniformly distributed across the days of the week.
- Alternative Hypothesis (H1): The number of orders is not uniformly distributed across the days of the week.
-
Perform Chi-Square Test:
-
Calculate the expected frequency of orders for each day if the distribution were uniform (total orders / 7).
-
Calculate the Chi-Square test statistic using the formula:
χ2 = Σ [(Observed Frequency – Expected Frequency)2 / Expected Frequency]
-
Determine the degrees of freedom (df = number of categories – 1 = 7 – 1 = 6).
-
Find the critical value from the Chi-Square distribution table for df = 6 and α = 0.05.
-
Compare the calculated Chi-Square statistic to the critical value.
-
-
Interpret Results:
- If the calculated Chi-Square statistic is greater than the critical value, reject the null hypothesis. This indicates that the distribution of orders is not uniform.
- If the calculated Chi-Square statistic is less than the critical value, fail to reject the null hypothesis. This indicates that the distribution of orders is uniform.
-
5.5 Advantages and Limitations of Statistical Tests
Advantages:
- Objectivity: Statistical tests provide an objective way to determine the distribution type, reducing reliance on subjective visual assessments.
- Quantifiable Results: They provide quantifiable results (p-values) that can be compared against a predefined significance level.
Limitations:
- Assumptions: Many tests have underlying assumptions that must be met for the results to be valid.
- Sample Size: The power of the tests depends on the sample size. Small sample sizes may not provide enough evidence to reject the null hypothesis, even if the data deviates from the specified distribution.
- Context: Statistical tests should be used in conjunction with visual assessments and domain knowledge to provide a comprehensive understanding of the data.
6. Practical Examples in Different Business Scenarios
Understanding whether data follows a normal or uniform distribution can significantly impact business decisions across various sectors. Here are practical examples:
6.1 Retail Inventory Management
- Scenario: A retail store wants to optimize its inventory levels by analyzing the demand for different products.
- Normal Distribution: If the demand for a particular product (e.g., a specific size of uniform) follows a normal distribution, the store can use this information to determine the optimal stock level. They can ensure that they have enough stock to meet the average demand while minimizing the risk of overstocking.
- Uniform Distribution: If the demand for a product (e.g., different colors of the same uniform) is uniformly distributed, the store can maintain equal stock levels for each color, ensuring that customers have a consistent selection.
6.2 Healthcare Appointment Scheduling
- Scenario: A clinic wants to improve its appointment scheduling process to minimize patient waiting times.
- Normal Distribution: If the duration of patient appointments follows a normal distribution, the clinic can use this information to allocate appointment slots more efficiently. They can schedule longer appointments for patients who are likely to require more time, based on historical data.
- Uniform Distribution: If the arrival times of patients are uniformly distributed throughout the day, the clinic can allocate staff resources evenly across the day, ensuring that there are enough personnel to handle patient flow at any given time.
6.3 Manufacturing Quality Control
- Scenario: A manufacturing company wants to monitor the quality of its products by analyzing various parameters.
- Normal Distribution: If a critical parameter (e.g., the length of a manufactured part) follows a normal distribution, the company can set control limits based on the mean and standard deviation. Deviations from this distribution may indicate a problem with the manufacturing process.
- Uniform Distribution: If the occurrence of defects is uniformly distributed across different production batches, the company can implement consistent quality control measures across all batches, ensuring that no batch is overlooked.
6.4 Finance Risk Assessment
- Scenario: A financial institution wants to assess the risk associated with different investment portfolios.
- Normal Distribution: If the returns of an investment portfolio follow a normal distribution, the institution can use this information to calculate the probability of different return scenarios and assess the risk accordingly.
- Uniform Distribution: If the occurrence of market events (e.g., economic recessions) is uniformly distributed over time, the institution can prepare for these events by diversifying its portfolio and implementing risk management strategies.
6.5 Human Resources Performance Evaluation
- Scenario: A company wants to evaluate the performance of its employees based on various metrics.
- Normal Distribution: If employee performance on a specific metric (e.g., sales volume) follows a normal distribution, the company can identify high-performing and low-performing employees relative to the average.
- Uniform Distribution: If the distribution of employee absenteeism is uniform across different departments, the HR department can implement consistent attendance policies across all departments, ensuring fairness and consistency.
6.6 Optimizing Online Uniforms Operations
- Uniform Sizing: If onlineuniforms.net finds that requests for different uniform sizes are uniformly distributed, they can ensure equal stock levels for all sizes to meet customer demand effectively.
- Order Placement: Analyzing the time of day when orders are placed can reveal patterns. A uniform distribution might indicate that orders are placed randomly throughout the day, requiring consistent staffing levels.
7. Tools and Software for Histogram Analysis
Several tools and software packages are available for creating and analyzing histograms. These tools can help businesses visualize data, perform statistical tests, and make informed decisions.
7.1 Spreadsheet Software (e.g., Microsoft Excel, Google Sheets)
Spreadsheet software is a basic yet powerful tool for creating histograms and performing simple data analysis.
- Creating Histograms: Excel and Google Sheets have built-in histogram functions that allow users to create histograms from their data with just a few clicks.
- Basic Statistics: These tools can also calculate basic statistics such as mean, median, standard deviation, and percentiles, which are useful for understanding the distribution of data.
7.2 Statistical Software (e.g., SPSS, SAS, R)
Statistical software packages offer more advanced features for data analysis, including a wider range of statistical tests and customization options.
- Advanced Statistical Tests: SPSS, SAS, and R can perform a variety of statistical tests for normality and uniformity, such as the Shapiro-Wilk test, Kolmogorov-Smirnov test, and Chi-Square test.
- Customization: These tools allow users to customize the appearance of histograms and create more complex visualizations.
- Data Manipulation: Statistical software packages also provide powerful data manipulation capabilities, allowing users to clean, transform, and analyze data more effectively.
7.3 Data Visualization Tools (e.g., Tableau, Power BI)
Data visualization tools are designed to create interactive and visually appealing dashboards that can help businesses understand their data at a glance.
- Interactive Histograms: Tableau and Power BI allow users to create interactive histograms that can be filtered and drilled down into to explore the data in more detail.
- Integration with Other Data Sources: These tools can connect to a wide range of data sources, allowing businesses to analyze data from multiple sources in one place.
- Collaboration: Data visualization tools also facilitate collaboration by allowing users to share dashboards and insights with colleagues.
7.4 Programming Languages (e.g., Python with Libraries like Matplotlib, Seaborn)
Programming languages like Python offer a flexible and powerful way to create and analyze histograms.
- Customization: Python libraries like Matplotlib and Seaborn allow users to create highly customized histograms and visualizations.
- Statistical Analysis: Python also has libraries like SciPy and Statsmodels that provide a wide range of statistical tests for normality and uniformity.
- Automation: Python can be used to automate the process of creating and analyzing histograms, making it easier to work with large datasets.
7.5 Selecting the Right Tool
The choice of tool depends on the specific needs and resources of the business:
- Small Businesses: May find spreadsheet software or basic data visualization tools sufficient for their needs.
- Large Enterprises: With more complex data analysis requirements may benefit from using statistical software or programming languages.
7.6 How Online Uniforms Utilizes Histogram Analysis Tools
At onlineuniforms.net, we leverage a combination of these tools to gain insights from our data:
- Excel: Used for basic data analysis and creating simple histograms to monitor uniform sales and customer demographics.
- Tableau: Used to create interactive dashboards that allow us to track key performance indicators and identify trends in our business.
- Python: Used for more advanced statistical analysis and automation of data analysis tasks.
8. Common Mistakes to Avoid When Interpreting Histograms
Interpreting histograms accurately is crucial for making informed decisions. Here are common mistakes to avoid:
8.1 Incorrect Bin Size Selection
- Mistake: Choosing a bin size that is too large or too small.
- Impact: A bin size that is too large can hide important details in the data, while a bin size that is too small can create a noisy histogram that is difficult to interpret.
- Solution: Experiment with different bin sizes to find one that provides a clear and accurate representation of the data. A common rule of thumb is to use the square root of the number of data points as the number of bins.
8.2 Ignoring the Context of the Data
- Mistake: Interpreting a histogram without considering the context of the data.
- Impact: The same histogram can have different interpretations depending on the context. For example, a histogram of customer ages may have different implications for a clothing store versus a retirement home.
- Solution: Always consider the context of the data when interpreting a histogram. Ask questions such as: What does the data represent? What is the source of the data? What are the potential biases in the data?
8.3 Confusing Correlation with Causation
- Mistake: Assuming that a correlation between two variables implies causation.
- Impact: Just because two variables are correlated does not mean that one variable causes the other. There may be other factors at play.
- Solution: Be cautious when interpreting correlations. Consider other potential explanations for the relationship between the variables.
8.4 Overgeneralizing from the Data
- Mistake: Drawing conclusions about the entire population based on a sample of the data.
- Impact: The sample may not be representative of the population as a whole, leading to inaccurate conclusions.
- Solution: Be careful when generalizing from the data. Consider the size and representativeness of the sample.
8.5 Neglecting Outliers
- Mistake: Ignoring outliers in the data.
- Impact: Outliers can have a significant impact on the shape of the histogram and can distort the interpretation of the data.
- Solution: Investigate outliers to determine whether they are legitimate data points or errors. If they are legitimate data points, consider whether they should be included in the analysis.
8.6 Failing to Consider Skewness
- Mistake: Ignoring the skewness of the distribution.
- Impact: Skewness can affect the interpretation of the data and can lead to inaccurate conclusions about the central tendency and variability of the data.
- Solution: Pay attention to the skewness of the distribution. If the distribution is skewed, consider using measures of central tendency and variability that are less sensitive to skewness, such as the median and interquartile range.
8.7 Practical Tips for Avoiding Mistakes
- Visualize the Data: Always create a histogram of the data to get a visual sense of the distribution.
- Calculate Descriptive Statistics: Calculate basic descriptive statistics such as mean, median, standard deviation, and percentiles to understand the central tendency and variability of the data.
- Perform Statistical Tests: Perform statistical tests to determine whether the data follows a normal or uniform distribution.
- Consider the Context: Always consider the context of the data when interpreting a histogram.
- Be Cautious When Generalizing: Be careful when generalizing from the data.
- Investigate Outliers: Investigate outliers to determine whether they are legitimate data points or errors.
8.8 Ensuring Accurate Interpretation at Online Uniforms
At onlineuniforms.net, we emphasize the importance of accurate histogram interpretation to ensure that our decisions are based on sound data analysis. We provide training to our employees on how to avoid common mistakes and use histograms effectively.
9. Advanced Techniques for Distribution Analysis
Beyond basic histogram analysis and statistical tests, several advanced techniques can provide deeper insights into data distributions.
9.1 Kernel Density Estimation (KDE)
- Description: KDE is a non-parametric technique used to estimate the probability density function of a random variable. It provides a smooth estimate of the distribution, without making assumptions about the underlying distribution type.
- Benefits:
- Smoothness: KDE produces a smooth estimate of the distribution, which can be easier to interpret than a histogram.
- Non-Parametric: KDE does not assume that the data follows a specific distribution, making it suitable for analyzing data with unknown distributions.
- Adaptability: KDE can adapt to the shape of the data, capturing complex patterns and features.
- Applications: KDE can be used to visualize and compare distributions, identify modes and clusters, and estimate probabilities.
9.2 Mixture Models
- Description: Mixture models are probabilistic models that assume the data is generated from a mixture of two or more underlying distributions.
- Benefits:
- Flexibility: Mixture models can model data with complex distributions that cannot be easily described by a single distribution.
- Interpretability: Mixture models provide insights into the underlying components of the data, which can be useful for understanding the data generation process.
- Clustering: Mixture models can be used for clustering data, by assigning each data point to the most likely component of the mixture.
- Applications: Mixture models can be used to analyze data with multiple modes or clusters, such as customer segmentation, image recognition, and genetics.
9.3 Quantile-Quantile (Q-Q) Plots
- Description: Q-Q plots are graphical tools used to compare the quantiles of two distributions. They plot the quantiles of the sample data against the quantiles of a theoretical distribution (e.g., normal or uniform).
- Benefits:
- Visual Comparison: Q-Q plots provide a visual way to assess how well the sample data fits the theoretical distribution.
- Detection of Deviations: Q-Q plots can detect deviations from the theoretical distribution, such as skewness, kurtosis, and outliers.
- Distribution Selection: Q-Q plots can be used to compare the fit of different theoretical distributions to the sample data.
- Applications: Q-Q plots are commonly used to assess the normality of data, but they can also be used to compare the fit of other distributions, such as uniform, exponential, and gamma.
9.4 Time Series Analysis
- Description: Time series analysis is a statistical technique used to analyze data that is collected over time. It involves identifying patterns and trends in the data and using this information to make predictions about future values.
- Benefits:
- Trend Identification: Time series analysis can identify trends, seasonality, and cycles in the data.
- Forecasting: Time series analysis can be used to forecast future values of the data.
- Anomaly Detection: Time series analysis can detect anomalies or outliers in the data.
- Applications: Time series analysis is commonly used in finance, economics, and engineering to analyze data such as stock prices, sales figures, and weather patterns.
9.5 Practical Applications for Online Uniforms
- KDE for Sizing Analysis: onlineuniforms.net can use KDE to analyze the distribution of uniform sizes ordered by customers. This can help them identify the most popular sizes and adjust their inventory accordingly.
- Mixture Models for Customer Segmentation: onlineuniforms.net can use mixture models to segment customers based on their purchasing behavior. This can help them tailor their marketing efforts and product offerings to different customer segments.
- Q-Q Plots for Quality Control: onlineuniforms.net can use Q-Q plots to assess the normality of product dimensions and ensure that their products meet quality standards.
- Time Series Analysis for Demand Forecasting: onlineuniforms.net can use time series analysis to forecast demand for different uniform types. This can help them optimize their production and inventory levels.
10. Conclusion: Enhancing Business Decisions with Distribution Analysis
Understanding how to tell if a histogram is normal or uniform is crucial for effective data analysis and informed decision-making across various business functions. By accurately interpreting data distributions, businesses can optimize processes, improve quality control, and enhance customer satisfaction.
10.1 Key Takeaways
- Histograms are powerful tools for visualizing data distributions.
- Normal distributions are characterized by a bell-shaped curve, while uniform distributions have a rectangular shape.
- Statistical tests such as the Shapiro-Wilk test and Chi-Square test can be used to determine the distribution type rigorously.
- Avoiding common mistakes in histogram interpretation is essential for accurate analysis.
- Advanced techniques like KDE, mixture models, and Q-Q plots can provide deeper insights into data distributions.
10.2 Integrating Distribution Analysis at Online Uniforms
At onlineuniforms.net, we are committed to leveraging distribution analysis to drive business success. By integrating these techniques into our operations, we can:
- Optimize inventory levels to meet customer demand effectively.
- Improve production planning to ensure a balanced output across all uniform sizes.
- Enhance quality control to maintain consistent product standards.
- Forecast demand to optimize production and inventory levels.
- Segment customers to tailor marketing efforts and product offerings.
By understanding the distribution patterns in our data, we can make data-driven decisions that lead to increased efficiency, improved customer satisfaction, and enhanced profitability.
10.3 Future Trends in Distribution Analysis
As data continues to grow in volume and complexity, the importance of distribution analysis will only increase. Future trends in this field include:
- Artificial intelligence (AI): AI algorithms can automate the process of distribution analysis, making it easier for businesses to extract insights from their data.
- Big data analytics: Big data analytics platforms can handle large datasets and perform complex distribution analysis tasks.
- Real-time analytics: Real-time analytics tools can provide up-to-the-minute insights into data distributions, allowing businesses to respond quickly to changing conditions.
10.4 Final Thoughts
Mastering the art of distribution analysis empowers businesses to unlock valuable insights hidden within their data. Whether it’s optimizing inventory, improving quality control, or forecasting demand, understanding data distributions is a key ingredient for success in today’s data-driven world.
Are you ready to leverage the power of distribution analysis for your business? Visit onlineuniforms.net today to explore our wide range of uniform solutions and discover how we can help you optimize your operations! Contact us at +1 (214) 651-8600 or visit our location at 1515 Commerce St, Dallas, TX 75201, United States to learn more.
FAQ: Understanding Histograms
1. What is the primary purpose of a histogram?
The primary purpose of a histogram is to visually represent the distribution of a dataset, showing the frequency of data points within specified ranges or bins.
2. How does a normal distribution appear on a histogram?
A normal distribution appears as a bell-shaped curve on a histogram, with the highest point at the mean and symmetrical tails tapering off on both sides.
3. What are the key characteristics of a uniform distribution in a histogram?
A uniform distribution is characterized by a rectangular shape with a flat top, indicating that all values within the range have an equal probability of occurring.
4. What statistical tests can be used to check for normality?
Statistical tests such as the Shapiro-Wilk test, Kolmogorov-Smirnov test, and Anderson-Darling test can be used to assess whether a dataset follows a normal distribution.
5. How can a Chi-Square test be used to determine uniformity?
A Chi-Square test compares the observed frequencies of data points in each bin to the expected frequencies under a uniform distribution, helping to determine if the data is uniformly distributed.
6. What is the impact of choosing an incorrect bin size in a histogram?
An incorrect bin size can either hide important details (if too large) or create a noisy histogram (if too small), making it difficult to interpret the data accurately.
7. What are some common mistakes to avoid when interpreting histograms?
Common mistakes include ignoring the context of the data, confusing correlation with causation, overgeneralizing from the data, and neglecting outliers.
8. How can kernel density estimation (KDE) enhance distribution analysis?
Kernel density estimation provides a smooth estimate of the distribution, without making assumptions about the underlying distribution type, offering a more detailed view than a basic histogram.
9. What are mixture models and how are they used in data analysis?
Mixture models are probabilistic models that assume data is generated from a mixture of two or more underlying distributions, useful for analyzing data with complex distributions.
10. How can Q-Q plots be used to compare distributions?
Q-Q plots compare the quantiles of two distributions, providing a visual way to assess how well the sample data fits a theoretical distribution like normal or uniform.